回溯法示例

回溯法

解决一个回溯问题，实际上就是一个决策树的遍历过程

模板：

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

其核心就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」

类比树的前序遍历和后序遍历，前序遍历即在递归方法前执行，后后序遍历则在递归方法结束后执行。

for 选择 in 选择列表:
    # 做选择
    将该选择从选择列表移除
    路径.add(选择)	#先序遍历
    backtrack(路径, 选择列表)	
    # 表示返回上一个节点，撤销选择
    路径.remove(选择)	#后序遍历
    将该选择再加入选择列表

全排列问题：

public class Permute {
    List<List<Integer>> res = new LinkedList<>();

    public static void main(String[] args) {
        Permute p=new Permute();
        int[] nums={1,2,3};
        p.permute(nums);
    }

    public void permute(int[] nums){
        LinkedList<Integer> track = new LinkedList<>();
        backtrack(nums,track);
        System.out.println(res);
    }

    public void backtrack(int[] nums, LinkedList<Integer> track) {
        // 路径：记录在 track 中
        // 选择列表：nums 中不存在于 track 的那些元素
        // 结束条件：nums 中的元素全都在 track 中出现
        if (track.size() == nums.length){
            res.add(new LinkedList<>(track));
            return;
        }
        for (int num : nums) {
            if (track.contains(num)){
                continue;
            }
            track.add(num); //做第一步选择
            backtrack(nums, track);
            //返回撤销上一步
            track.removeLast();
        }
    }
}

该全排列时间复杂度为O（n），且不管怎么优化，都不能小于O（n）。回溯算法不像动态规划存在重叠子问题可以优化，回溯算法就是纯暴力穷举，复杂度一般都很高。

剪枝函数： 当深度遍历到某节点时，发现该节点不满足条件，则跳过该节点及其子节点的遍历。

结果一定是要有一个全局参数来保存

image-20201116090206952

作业：素数环

​ 把整数{1, 2, …, 20}填写到一个环中，要求每个整数只填写一次，并且相邻的两个整数之和是一个素数。

思路：

​ 因为是一个环，因此设定从1开始，track用于保存已走路径，运用前一值加现有值是否为素数为剪枝函数，递归出口为所有数都添加到track中，得到全部结果。

package algorithm.backtrack;

import java.util.LinkedList;
import java.util.List;

public class PrimeRing {

    List<List<Integer>> res = new LinkedList<>();   //保存最终结果
    public static void main(String[] args) {
        PrimeRing primeRing = new PrimeRing();
        int[] initList=new int[20];
        for (int i = 0;i < initList.length; i++) {
            initList[i]=i+1;
        }
        primeRing.solve(initList);
    }

    public void solve(int[] nums){
        LinkedList<Integer> track = new LinkedList<>();
        track.add(nums[0]);
        backTracking(nums,track);
        System.out.println("所有排列为："+res);
        System.out.println("显示了前"+res.size()+"种排列");
    }

    int preNum=1;    // 记录前一个路径节点值
    public void backTracking(int[] nums,LinkedList<Integer> track){
        // 路径：记录在 track 中
        // 选择列表：nums 中不存在于 track 的那些元素
        // 结束条件：nums 中的元素全都在 track 中出现

        // 由于20的所有情况种数太多，这里只打印前100种结果
        if (res.size() == 10000){
            return;
        }
        if (track.size()== nums.length){    //所有数均遍历过则退出
            //判断首位和是否为素数
            if (isPrime(track.getLast(), track.getFirst())){
                res.add(new LinkedList<>(track));
            }
            return;
        }
        for (int i = 1; i < nums.length; i++) {
            //已添加过则跳过
            if (track.contains(nums[i])){
                continue;
            }
            //如果与前一数和为素数则尝试添加
            if (isPrime(preNum,nums[i])){
                track.add(nums[i]);
                //记录前一位置的数
                preNum=nums[i];
                backTracking(nums, track);
                //撤销并修改前一位置的数
                track.removeLast();
                preNum=track.getLast();
            }
        }
    }

    /**
     * 判断是否为素数
     * @param a
     * @param b
     * @return
     */
    public static boolean isPrime(int a,int b){
        int c=a+b;
        for (int i = 2; i <= Math.sqrt(c); i++) {
            if (c%i==0){
                return false;
            }
        }
        return true;
    }
}

image-20201120104834865

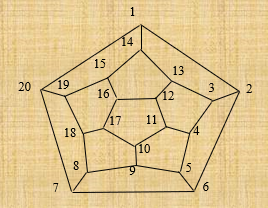
作业：哈密顿环

​ 著名的爱尔兰数学家哈密顿提出了著名的周游世界问题。正十二面体的20个顶点代表20个城市，要求从一个城市出发，经过每个城市恰好一次，然后回到出发城市。

image-20201116123204656

思路：

与上题思路相似，从设定的起点开始采用深度遍历dfs，如果无法继续遍历则回溯，直到遍历完所有节点。路径保存到track中。

//采用邻接表存储图
public class Graph {
    final static int[] p1 = {2,14,20};
    final static int[] p2 = {1,3,6};
    final static int[] p3 = {2,4,13};
    final static int[] p4 = {3,5,11};
    final static int[] p5 = {4,6,9};
    final static int[] p6 = {2,5,7};
    final static int[] p7 = {6,8,20};
    final static int[] p8 = {7,9,18};
    final static int[] p9 = {5,8,10};
    final static int[] p10 = {9,11,17};
    final static int[] p11 = {4,10,12};
    final static int[] p12 = {11,13,16};
    final static int[] p13 = {3,12,14};
    final static int[] p14 = {1,13,15};
    final static int[] p15 = {14,16,19};
    final static int[] p16 = {12,15,17};
    final static int[] p17 = {10,18,16};
    final static int[] p18 = {5,17,19};
    final static int[] p19 = {15,18,20};
    final static int[] p20 = {1,7,19};
    public final static int[][] graph = {p1,p2,p3,p4,p5,p6,p7,p8,p9,p10,p11,p12,p13,p14,p15,p16,p17,p18,p19,p20};
}

package algorithm.backtrack.hamiltonianGraph;

import java.util.Arrays;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.List;
import java.util.stream.Collectors;

public class HamiltonianGraph {

    public HamiltonianGraph(){
        initgraph();
    }

    private static int startNum;  //选择开始节点
    HashMap<Integer,int[]> graph= new HashMap<>();  //保存图的临接表
    List<List<Integer>> res = new LinkedList<>();   //保存最终结果

    public static void main(String[] args) {
        HamiltonianGraph hamiltonianGraph = new HamiltonianGraph();
        startNum=1;
        hamiltonianGraph.solve(startNum);  //起始节点
    }

    public void solve(int startNode){
        LinkedList<Integer> track = new LinkedList<>(); //保存已走过的路径
        track.add(startNode);
        backTracking(track,startNode);
        System.out.println("所有能走的路径为：");
        res.forEach(System.out::println);
        System.out.println("一共有"+res.size()+"种方法");
    }

    private void backTracking(LinkedList<Integer> track,int startNode) {
        // 递归出口：所有节点都已存放到track中
        if (track.size() == graph.size()) {
            // 判断最后一个节点是否为开始结点的邻接点
            // 如果是开始结点的邻接点，则添加到结果里
            if (Arrays.stream(Graph.graph[startNum - 1]).boxed().collect(Collectors.toList()).contains(track.getLast())) {
                res.add(new LinkedList<>(track));
            }
            return;
        }
        //获取当前节点的邻接表
        int[] nodes = graph.get(startNode);
        for (int num:nodes){
            if (track.contains(num)){
                continue;
            }
            //尝试加入到路径
            track.add(num);
            backTracking(track,num);
            //撤销并返回上一步
            track.removeLast();
        }
    }

    /**
     * 初始化图存入HashMap
     */
    public void initgraph(){
        for (int i = 0; i <20; i++) {
            graph.put(i+1, Graph.graph[i]);
        }
    }

}

image-20201120104921142

体会：

​ 通过这两个题目，我对回溯法的理解更加深刻了一些。

​ 解决一个回溯问题，实际上就是一个决策树的遍历过程，而回溯法相对于穷举法的优势在于，加入了剪枝函数，使得运行效率得到了提高。其核心就是 for 循环里面的递归，在递归调用之前做选择，在递归调用之后撤销选择。类比树的前序遍历和后序遍历，前序遍历即在递归方法前执行，后序遍历则在递归方法结束后执行。但是回溯法不像动态规划存在重叠子问题可以优化，回溯算法就是纯暴力穷举，复杂度一般都很高。

​ 两题的时间复杂度为O（n），且使用回溯法不管怎么优化，都不能小于O（n）。

分支限界法

与回溯法对比

回溯法是对解空间深度优先搜索，分支限界法是对解空间广度优先搜索。

对于具有指数阶个数节点的解空间树，在最坏情况下，时间复杂度肯定为指数阶

算法思想

• 按照BFS原则，一个活结点R成为E-结点（扩展结点）
• 依次将R的全部孩子结点加入到活结点表中
• R自身成为死结点
• 从新的活结点表中选一个活结点作为E-结点

image-20201123081706790

根据之后不同的搜索方法，可以将分支限界法划分为三种：

FIFOBB（先进先出法）-->队列

先广后深

FIFO求解四皇后问题的流程。L1、L2···代表当前结点成为死结点后的活结点队列。

image-20201123083600892

LIFOBB（后进先出法）-->栈

先遍历完一颗子树、才能遍历兄弟结点的子树。（回到了BFS）

LCBB（优先队列式法）-->堆（最大堆最小堆）

最小代价/最大效益（LC）优先

代价函数值C(·)作为出队优先权

结点处代价函数值

image-20201123085352649

相对代价函数g(·)

衡量一个结点X的相对代价有两种标准：

• 在生成一个答案结点以前，子树X上需要生成的结点数目
  • 采用此标准，总是生成最小数目的结点。
• 在子树X上，离X最近的答案结点到X的路径长度
  • 采用此标准，则要成为E-结点的结点只是由根到最近的那个答案结点路径上的那些结点

采用标准1：各结点的g(x)值如下：

image-20201123090417612

采用标准2：各结点的g(x)值如下：

image-20201123090523914

计算结点代价

难度与求得问题最优解的难度相当

c(X)=f(X)+g(X)

其中f(X)固定，即c(X)的大小取决与g(X).

但是g(X)的计算是很难的，当只有找到答案结点的时候，才有可能计算出g(X)，因此复杂度很高。

相对代价估计函数

因此相对代价函数不必求出具体的值，对它进行估计即可 \[ g^{-}(·) \] 满足如下特性:

• 如果Y是X的孩子，则有 \[ g^{-}(Y)\leq g^{-}(X) \]