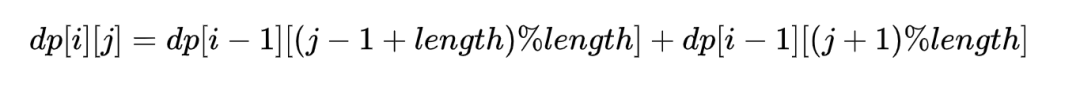LeetCode中等算法题记录

1.打家劫舍3（动态规划）*

image-20210715223605747

解法一

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
  // 使用map存储节点已经计算过的值
    Map<TreeNode, Integer> map = new HashMap<>();
    public int rob(TreeNode root) {
        if (root == null) return 0;    
      // 多了下面这句代码，效率提升100倍
        if (map.containsKey(root)) return map.get(root);
        int money = root.val;
        if (root.left != null) {
            money += rob(root.left.left) + rob(root.left.right);
        }
        if ( root.right != null) {
            money += rob(root.right.left) + rob(root.right.right);
        }
        int res = Math.max(money, rob(root.left) + rob(root.right));
        map.put(root, res);
        return res;
    }
}

由于在偷爷爷的时候，会计算孙子能偷到的钱，其中也会计算到儿子能偷到的钱。所以递归到儿子成为爷爷的时候，就不需要再继续计算了，而是直接从map里面拿，跟斐波那契数列的去重非常相似。

非常妙的是，下一层的money返回后会加到上一层的money上，所以返回到最终，money就是下面节点累加的值。

解法二

对每个节点都生成一个一维数组，大小为2，代表偷它能得到最大的钱和不偷它能得到最大的钱。递归的时候从叶子结点返回，依此给每个节点的数组进行赋值，最后我们只需要返回偷根节点和不偷根节点谁能获得更多即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int rob(TreeNode root) {
        if (root == null) return 0;
        int[] res = robOrNot(root);
        return Math.max(res[0], res[1]);
    }
    public int[] robOrNot(TreeNode root) {
        if (root == null) return new int[2];
        int[] result = new int[2];
        // 左孩子的结果
        int[] left = robOrNot(root.left);
        // 右孩子的结果
        int[] right = robOrNot(root.right);

        // 给当前节点赋值，偷当前节点，不能偷左右孩子
        result[0] = root.val + left[1] + right[1];
        // 不偷当前节点,选择左右孩子节点最佳组合
        result[1] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);

        return result;
    }
}

小结

树形的动态规划做得非常少，线性的我们通常用数组进行存储，树形的由于不能索引，我们就使用Map来存储，其实本质都是一样，能够记录之前的结果并且复用。

2.红黑树

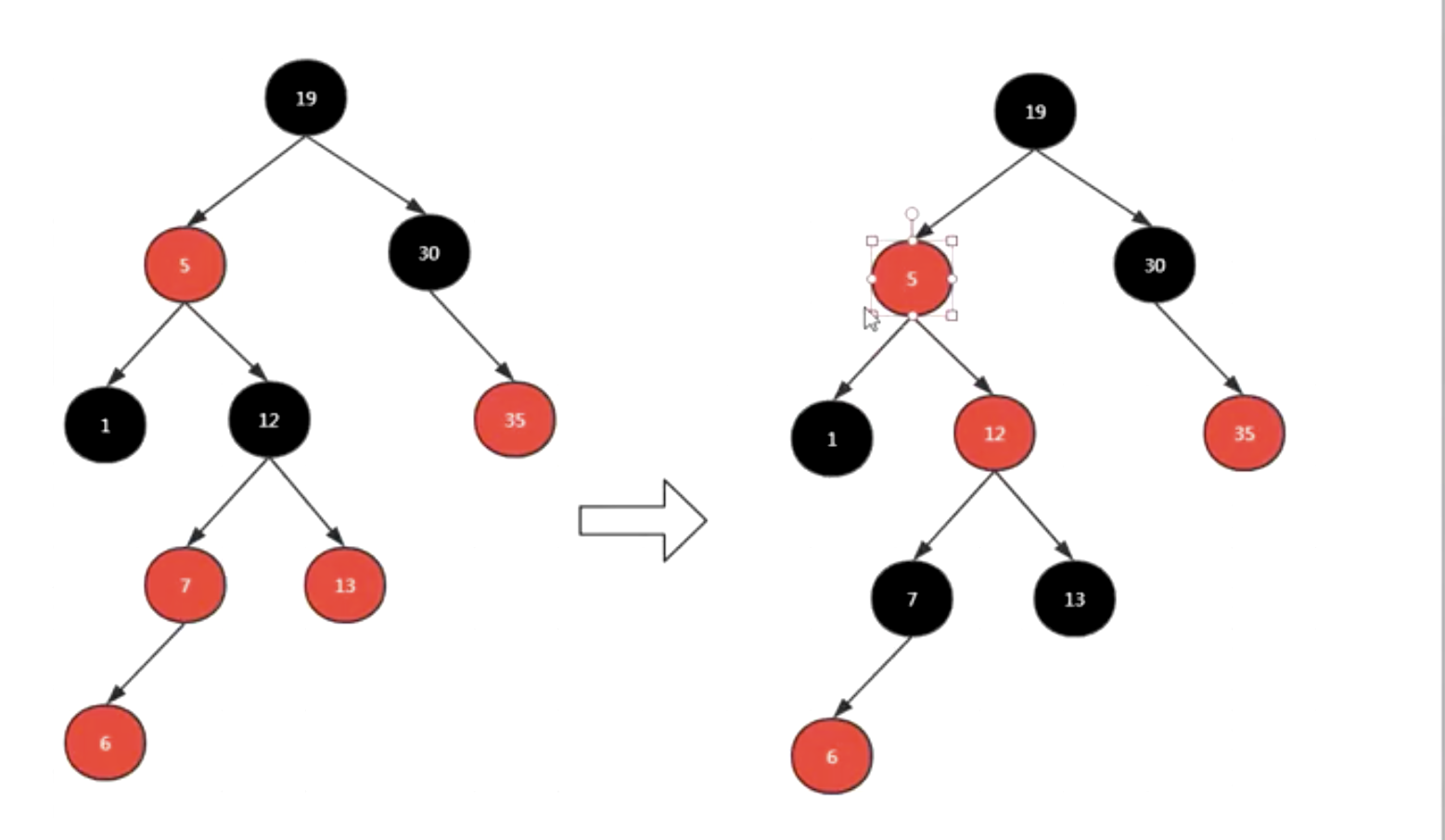
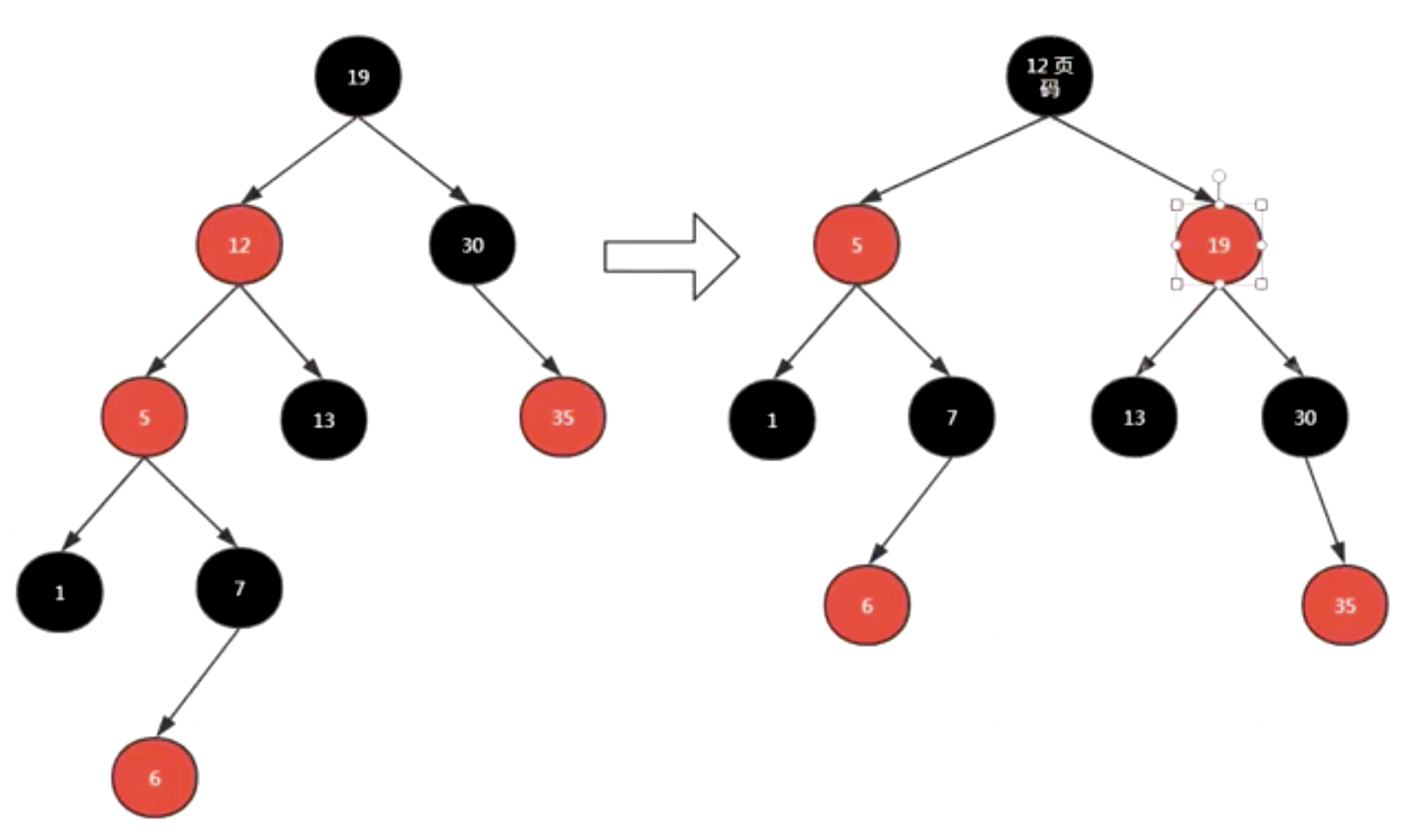
所有插入的点默认为红色。

变颜色的条件：插入的红色节点的父亲节点和叔叔节点都是红色的时候。

（父亲是红色，儿子也是红色不干，插入的儿子是红色后，父亲和叔叔都变成黑色，区分辈分，爷爷也要从黑色变成红色，区分辈分）

image-20210718215331500
image-20210718220001335
image-20210718220226766

3.零钱兑换（完全背包最值）*

image-20210718225517361

典型的01完全背包，dp[i]表示组成金额为i，最少需要多少枚硬币。括号里第一个dp[i]如果小，表示无法组成，dp[i - coins[i]] + 1表示当前金额减去当前硬币金额后所需的最少数量已经计算出来了，而且当前硬币金额小于amout，可以兑换一个，那么+1；

注意点是dp[]大小要设置成amount+1，不能是amount，会导致少算一次。

然后在初始化的时候第一次用Integer.MAX_VALUE，后面+1后就溢出了，不好判断。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    // dp[i] = min(dp[i], dp[i - coins[i]] + 1);
    public int coinChange(int[] coins, int amount) {
        int max = amount + 1;
        int[] dp = new int[amount + 1];
        Arrays.fill(dp, max);
        dp[0] = 0;
        for (int i= 1; i <= amount; i++) {
            for (int coin : coins) {
                if (i >= coin) {
                    dp[i] = Math.min(dp[i], dp[i-coin] + 1);
                }
            }        
        }

        return dp[amount] > amount ? -1 : dp[amount];
    }
}

4.变位数组

image-20210718232550508 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public List<List<String>> groupAnagrams(String[] strs) {
        Map<String,List<String>> map = new HashMap<>();

        for (String s : strs) {
            char[] chars = s.toCharArray();
            Arrays.sort(chars);
          // 对每个字符串进行排序
            String newStr = String.valueOf(chars);
            List<String> list = map.getOrDefault(newStr, new ArrayList<>());
            list.add(s);
            map.put(newStr, list);
        }
        List<List<String>> res = new ArrayList<>();
        for (Map.Entry<String, List<String>> entry : map.entrySet()) {
            res.add(entry.getValue());
        }
        return res;
    }
}

5.除自身以外数组的乘积

image-20210720172007105 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {

    public int[] productExceptSelf(int[] nums) {
        int[] l = new int[nums.length];
        int[] r = new int[nums.length];
        l[0] = 1;
        for (int i = 1; i < nums.length;i++) {
            l[i] = l[i - 1] * nums[i-1];
        }
        r[nums.length - 1] = 1;
        for (int i = nums.length - 2; i >= 0;i--) {
            r[i] = r[i + 1] * nums[i + 1];
        }
        int[] res = new int[nums.length];
        for (int i = 0; i<nums.length; i++) {
            res[i] = l[i] * r[i];
        }
        return res;
    }
}

用左右数组保存索引为i的左右两边的乘积。

6.LRU 缓存设计（数据结构，优先队列）*

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
import java.util.*;


public class Solution {

    static class ListNode{
        int key;
        int value;
        ListNode pre;
        ListNode next;
        public ListNode(){};
        public ListNode(int key, int value) {
            this.key = key;
            this.value = value;
        }
    }
    private Map<Integer, ListNode> map = new HashMap<>();
    int size = 0;
    int cap;
    final ListNode head = new ListNode(-1,-1);
    final ListNode tail = new ListNode(-1,-1);
    public Solution() {
        head.next = tail;
        tail.pre = head;
    }
    /**
     * lru design
     * @param operators int整型二维数组 the ops
     * @param k int整型 the k
     * @return int整型一维数组
     */
    public int[] LRU (int[][] operators, int k) {
        this.cap = k;
        // write code here
        int m = operators.length;
        int n = operators[0].length;
        // 要打印的次数
        int len = (int)Arrays.stream(operators).filter(x -> x[0] == 2).count();
        int[] res = new int[len];
        for (int i=0, j = 0;i < m ; i++) {
            if (operators[i][0] == 1) {
                // put
                put(operators[i][1],operators[i][2]);
            }else {
                // get
                res[j++] = get(operators[i][1]);
            }
        }
        return res;
    }

    public int get(int key) {
        ListNode node = map.get(key);
        if (node == null) {
            return -1;
        }
        // 移动到头部
        moveToHead(node);
        return node.value;
    }

    public void put(int key, int value) {
        ListNode node = map.get(key);
        // 不存在
        if (node == null) {
            node = new ListNode(key, value);
            addNode(node);
            // 添加到首部
            // 超过大小
            if (size > cap) {
                // 移除末尾
                removeNode(tail.pre);
            }
        }else {
            // 存在
            node.value = value;
            moveToHead(node);
        }
    }

    public void moveToHead(ListNode node) {
        removeNode(node);
        addNode(node);
    }
    // 删除节点
    public void removeNode(ListNode node) {
        node.pre.next = node.next;
        node.next.pre = node.pre;
        map.remove(node.key);
        size--;
    }
    // 添加到队首
    public void addNode(ListNode node) {
        node.pre = head;
        node.next = head.next;
        head.next.pre = node;
        head.next = node;
        map.put(node.key, node);
        size++;
    }

}

注意添加和删除的顺序，以及size++和size--的位置，把移动到队首分解为删除节点然后添加节点。

链表ListNode存储的是节点顺序，作用就是记录使用的长短，从队尾入队，队首出队。

HashMap存储的是(ListNode.key,ListNode)。

删除的时候记得链表和Map都要删除，但是size只是-1；

7.最小K个数（大根堆）

找出一组数的最小的k个数。

1
2
3
4
5
6
7
8
9
10
11
import java.util.*;

public class Solution {
    public ArrayList<Integer> GetLeastNumbers_Solution(int [] input, int k) {
        PriorityQueue<Integer> maxHeap = new PriorityQueue<>(k, (o1, o2) -> o2 - o1);
        for (int num : input) {
            maxHeap.offer(num);
        }
        return new ArrayList<>(maxHeap);
    }
}

使用大根堆进行操作，个数满了的时候移除掉最大的元素。

使用了

PriorityQueue<Integer> maxHeap = new PriorityQueue<>(k, (o1, o2) -> o2 - o1);lambda表达式，匿名Comparator，o2-o1表示从大到小。

8.二叉树层序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import java.util.*;
public class Solution {
    /**
     *
     * @param root TreeNode类
     * @return int整型ArrayList<ArrayList<>>
     */
    public ArrayList<ArrayList<Integer>> levelOrder (TreeNode root) {
        ArrayList<ArrayList<Integer>> res = new ArrayList();//用于返回最后的结果
        if(root == null) return res;//如果根节点为空就返回结果
        Queue<TreeNode> q = new LinkedList<TreeNode>();//用于存储每一层的节点
        q.add(root);
        while(!q.isEmpty()){
            int n = q.size();
            ArrayList<Integer> temp = new ArrayList<>();//用于存储当前遍历这一层的节点
            for(int i = 0;i < n;i ++){
                TreeNode node = q.poll();//取出队列的第一个元素
                temp.add(node.val);//将队头元素保存起来
                if(node.left != null) q.add(node.left);//左孩子如果不为空就进队列
                if(node.right != null) q.add(node.right);//右孩子如果不为空就进队列
            }
            res.add(temp);//将这一层的节点数里面据保存到res
        }
        return res;
    }
}

9.分割等和子集（背包问题）*

image-20210722225638064 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    // dp[i] : 0-i 能否填满容量为i的背包
    public boolean canPartition(int[] nums) {
        int sum = Arrays.stream(nums).sum();
        // 奇数不可能
        if (sum % 2 != 0) {
            return false;
        }
        int subSum = sum / 2;

        boolean[] dp = new boolean[sum];
        dp[0] =true;
        for (int i = 1; i < nums.length;i++) {
            for (int j = subSum; j >= nums[i];j--) {
                dp[j] = dp[j] || dp[j - nums[i]];
            }
        }

        return dp[subSum];
    }
}

10.背包问题总结

P、NP、NPC。

https://leetcode-cn.com/problems/coin-change/solution/yi-pian-wen-zhang-chi-tou-bei-bao-wen-ti-sq9n/

10.1背包问题分类

1、0/1背包问题：每个元素最多选取一次 2、完全背包问题：每个元素可以重复选择 3、组合背包问题：背包中的物品要考虑顺序 4、分组背包问题：不止一个背包，需要遍历每个背包

而每个背包问题要求的也是不同的，按照所求问题分类，又可以分为以下几种： 1、最值问题：要求最大值/最小值 2、存在问题：是否存在…………，满足………… 3、组合问题：求所有满足……的排列组合

因此把背包类型和问题类型结合起来就会出现以下细分的题目类型： 1、0/1背包最值问题 2、0/1背包存在问题 3、0/1背包组合问题 4、完全背包最值问题 5、完全背包存在问题 6、完全背包组合问题 7、分组背包最值问题 8、分组背包存在问题 9、分组背包组合问题 这九类问题我认为几乎可以涵盖力扣上所有的背包问题

10.1.1分类解题模板

背包问题大体的解题模板是两层循环，分别遍历物品nums和背包容量target，然后写转移方程， 根据背包的分类我们确定物品和容量遍历的先后顺序，根据问题的分类我们确定状态转移方程的写法

首先是背包分类的模板： 1、0/1背包：外循环nums数组,内循环target数组,target倒序且target>=nums[i]; 2、完全背包：外循环nums,内循环target,target正序且target>=nums[i]; 3、组合背包(考虑顺序)：外循环target,内循环nums,target正序且target>=nums[i]; 4、分组背包：这个比较特殊，需要三重循环：外循环背包bags,内部两层循环根据题目的要求转化为1,2,3三种背包类型的模板

然后是问题分类的模板： 1、最值问题: dp[i] = max/min(dp[i], dp[i-nums]+1)或dp[i] = max/min(dp[i], dp[i-num]+nums); 2、存在问题(bool)：dp[i]=dp[i]||dp[i-num]; 3、组合问题：dp[i]+=dp[i-num];

这样遇到问题将两个模板往上一套大部分问题就可以迎刃而解

10.2 0/1背包组合问题

https://leetcode-cn.com/problems/target-sum/

image-20210723163416186 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    // dp[i]:目标和为i有几种方法
    // dp[i] = dp[i] = dp[i] + dp[i-nums[j]]
    public int findTargetSumWays(int[] nums, int target) {
        if (nums == null || nums.length == 0) return 0;
        // 正数和x，负数和y， x+y = sum, x-y=target; x + x - target = sum. 
        // x = (target + sum) /2
        int sum = Arrays.stream(nums).sum();
        if ((sum + target) % 2 != 0 || sum < target) {
            return 0;
        }
        int xSum = (target + sum) / 2;
        int[] dp = new int[xSum + 1];
        dp[0] = 1;
        for (int num : nums) {
            for (int i = xSum; i >= num; i--) {
                dp[i] += dp[i - num];
            }
        }
        return dp[xSum];
    }
}

数组中包含正数和x，负数和y(y<0)，两部分加起来等于target。我们想要忽略掉负数和，因为dp数组表示负数不好表示。那么我们得到 x+y = target 此时x，y都是未知，那么我们需要替换掉一个，而x-y=sum，sum是很好求的，那么替换掉负数和y，x+x-target=sum,即x = (target+sum)/2。我们只需要求正数和为x的组合即可。

dp[i]就表示和为i的组合数。根据01组合背包的公式：dp[i]+=dp[i - num]，即可得到状态转移方程。

而01背包外层循环nums数组，内层反向循环target数组（0-x所有数字的数组）。

10.3 完全背包最值问题

https://leetcode-cn.com/problems/perfect-squares/

image-20210723171730997 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    // 完全背包最值问题,dp[i]:和为i对完全平方数最少数量
    // dp[i] = min(dp[i],dp[i-num * num] + 1)
    public int numSquares(int n) {
        if(n < 1) return 0;

        int[] dp = new int[n + 1];
        for(int i = 1;i <= n; i++) {
            dp[i] = i; // 最坏的情况每次都为1相加
            for (int j = 1;i - j * j >= 0; j++) {
                dp[i] = Math.min(dp[i], dp[i - j * j] + 1);
            }
        }   
        return dp[n];
    }

}

注意for循环内层的顺序，以及边界条件， i - j * j >=0表示将i从j^2开始减，直到i = 0减完。

11.单源最短路径

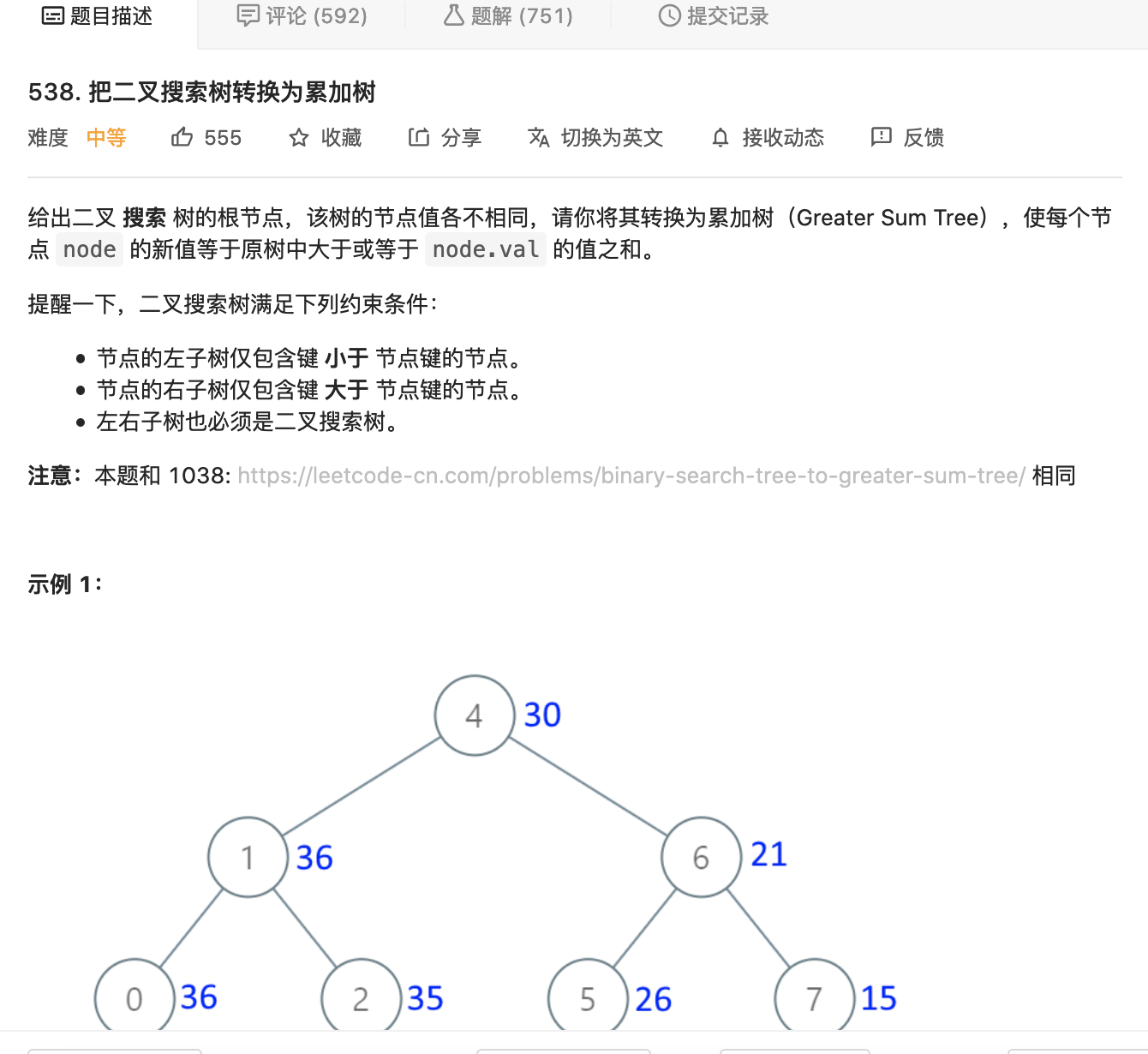
12.把二叉搜索树转换为累加树（中序遍历）

https://leetcode-cn.com/problems/convert-bst-to-greater-tree/

image-20210723173453761

即当前节点的值为，所有比当前节点值大的节点值之和。

二叉排序树中序遍历从小到大，那么逆中序遍历（非后序遍历）就是从大到小。然后我们将遍历过的节点依此相加到前一个节点就可以完成。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    // 记录比当前节点大的所有节点值的和
    int score = 0;
    public TreeNode convertBST(TreeNode root) {
        if (root == null) return null;
        if(root.right != null) {
            convertBST(root.right);
        }
        score += root.val;
        root.val =score;
        if (root.left != null) {
            convertBST(root.left);
        }
        return root;
    }

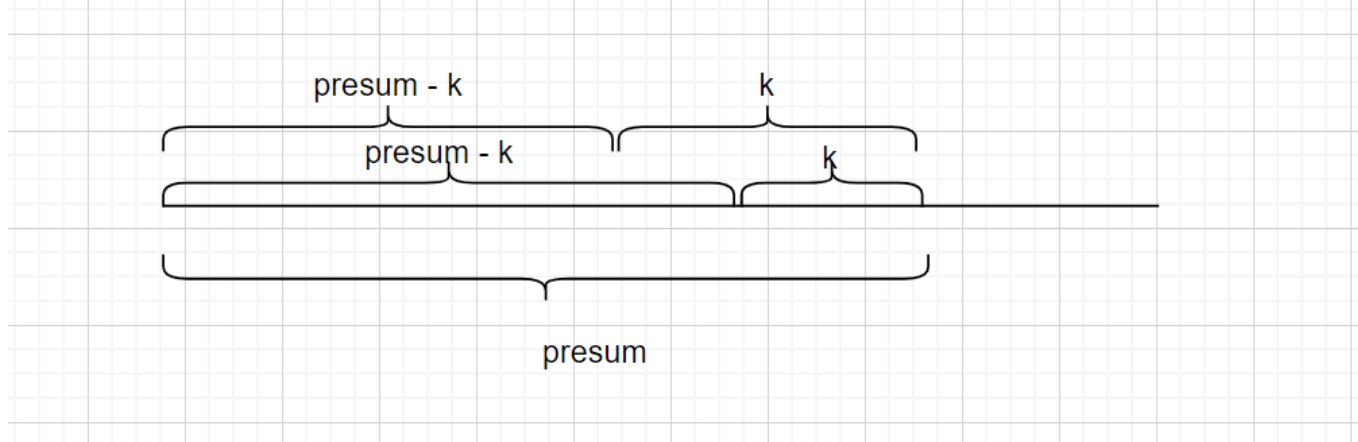
13.和为k的数组(前缀和)

https://leetcode-cn.com/problems/subarray-sum-equals-k/

image-20210723183823657

知识点：前缀和

前缀和+HashMap：时间复杂度（O(n)）。

跟两数之和类似，对于区间0-i,要得到k，只需要判断map是否包含0-i区间和减去k是否存在即可。类似两数之和只需要判断是否存在和减去当前数即可。

image-20210723183648913 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int subarraySum(int[] nums, int k) {
        if (nums == null) return 0;
        int count = 0;
        int n = nums.length;
        Map<Integer, Integer> map = new HashMap<>();
        //细节，这里需要预存前缀和为 0 的情况，会漏掉前几位就满足的情况
        //例如输入[1,1,0]，k = 2 如果没有这行代码，则会返回0,漏掉了1+1=2，和1+1+0=2的情况
        //输入：[3,1,1,0] k = 2时则不会漏掉
        //因为presum[3] - presum[0]表示前面 3 位的和，所以需要map.put(0,1),垫下底
        map.put(0, 1);
        int sum = 0;
        for (int num : nums) {
            sum += num;
            if (map.containsKey(sum - k)) {
                count += map.get(sum - k);
            }
            map.put(sum, map.getOrDefault(sum, 0) + 1);
        }
        return count;
    }
}

暴力枚举法：时间复杂度（O（n^2））

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int subarraySum(int[] nums, int k) {
        if (nums == null) return 0;
        int count = 0;
        for (int i = 0; i < nums.length; i++) {
            int sum = nums[i];
            if (sum == k) {
                count++;
            }
            for (int j = i+1; j < nums.length;j++) {
                sum += nums[j];
                if (sum == k) {
                    count++;
                }
            }
        }

        return count;
    }
}

14.找到字符串中所有字母异位词（滑动窗口）

image-20210724223335709

第一想法就是按照p的长度进行搜索，不过每次搜索为了判断是否一致都需要将数组排序后再转成字符串，时间复杂度O（n），但是耗时2200ms。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public List<Integer> findAnagrams(String s, String p) {
        List<Integer> res = new ArrayList<>();
        int m = s.length();
        int n = p.length();
        char[] pChars = p.toCharArray();
        Arrays.sort(pChars);
        String word = new String(pChars);
        for (int i = 0; i <= m - n;i++) {
            char[] sChars = s.substring(i, i + n).toCharArray();
            Arrays.sort(sChars);
            if (word.equals(new String(sChars))) {
                res.add(i);
                continue;
            }
        }
        return res;
    }
}

15.单调栈

单调栈分为单调递减栈和单调递增栈，什么场景用什么栈需要区分清楚。

判别是否需要使用单调栈，如果需要找到左边或者右边第一个比当前位置的数大或者小，则可以考虑使用单调栈；单调栈的题目如矩形米面积等等

image-20210724230857574

15.1 每日温度

image-20210725092454906

使用单调递增栈（栈顶到栈底）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        int n = temperatures.length;
        Stack<Integer> s = new Stack();
        int[] res = new int[n];
        for (int i = 0; i< n;i++) {
            int temperature = temperatures[i];
          // 如果当前元素比栈顶元素大，则找到了栈顶元素右边第一个大的值，可以给栈顶元素的res赋值。
            while(!s.isEmpty() && temperature > temperatures[s.peek()]) {
                int lastBigger = s.pop();
                res[lastBigger] = i - lastBigger;
            }
            s.push(i);
        }
        return res;
    }
}

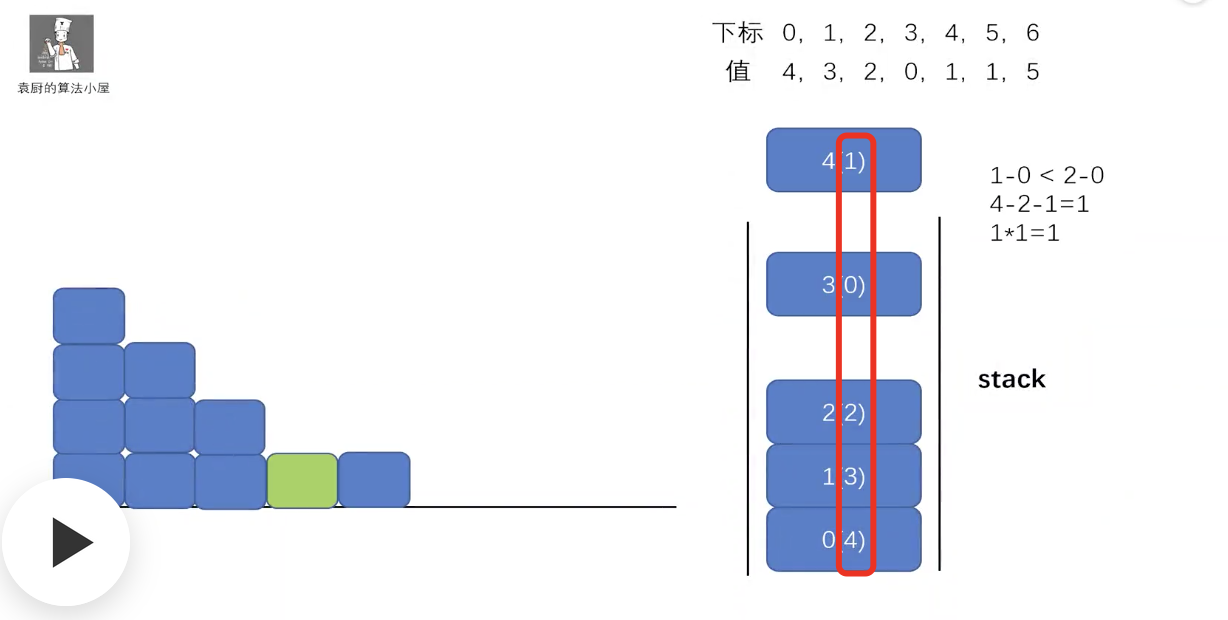
15.2 接雨水（hard）

image-20210725100710487

根据短板效应，使用递增栈，1、2、3、4、5；栈中存储的是索引，对应的高度由height[i]确定

image-20210725101233689

如果当前元素比栈顶小，则直接入栈。

如果当前元素比栈顶大，那么取出栈顶元素，肯定为低谷。

如当前栈元素为 2、3、4。那么取出的就是2；

然后再取出下一个栈顶元素（peek），即3； 那么当前元素、2、3就组成了一个坑洼.

然后就可以计算这个坑洼可以接多少水。

高度即（Math.min(当前元素高度-2), 3-2）;

宽度即坑洼底端的长度。即3的索引 - 当前位置索引 -1，如上图绿色位置的宽度即 4 - 2 - 1 = 1.

然后保存结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    // 递增栈 1\2\3\4\5 2
    public int trap(int[] height) {
        int n = height.length;
        Stack<Integer> s = new Stack();
        int res = 0;
        for (int i =0;i < n; i++) {
            // 当前元素比栈顶大 5 1 2
            while (!s.isEmpty() && height[i] > height[s.peek()]) {
                // 最矮的元素
                int popIdx = s.pop();
                // 比较当前元素、栈顶元素、下一个比当前栈高的元素

                // 有重复，如 1、1
                while(!s.isEmpty() && height[popIdx] == height[s.peek()]) {
                    s.pop();
                }
                if (!s.isEmpty()) {
                    // 比较高的元素
                    int temp = height[s.peek()];
                    // 短板高度
                    int resHeight = Math.min(height[i] - height[popIdx], temp - height[popIdx]);
                    // 宽度
                    int width = i - s.peek() - 1;
                    res += width * resHeight;
                }
            }
            s.push(i);
        }
        return res;
    }
}

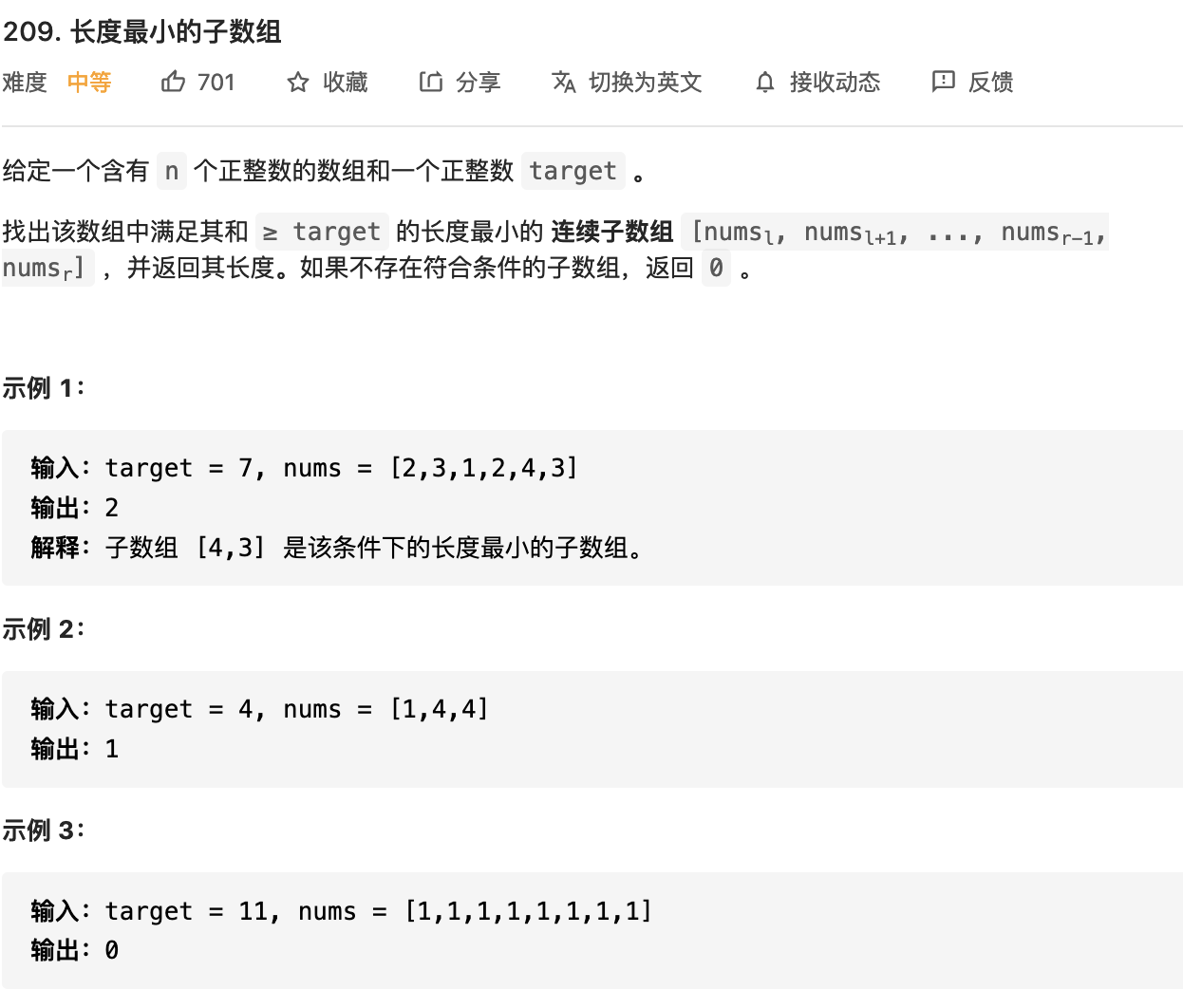
16.长度最小的子数组（滑动窗口、前缀和）

前缀和：数组前i个数的和组成新的数组。如果是正数，所以一般递增，可以考虑使用二分法。

涉及连续子数组的问题，我们通常有两种思路：一是滑动窗口、二是前缀和。

image-20210726171538696

只需要最小的长度，且子数组连续，可以使用滑动窗口，当sum < target的时候 right++，当sum == target的时候，取长度最小值，不结束，然后right++。当sum > target的时候，sum -= nums[left],left++;

注意边界值，退出的条件：right > nums.length

滑动窗口：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    // 
    public int minSubArrayLen(int target, int[] nums) {
        if (nums.length == 0) return 0;
        int left = 0;
        int right = 0;
        int minLength = 0;
        int n = nums.length;
        int sum = 0;
        while(right < n) {
            sum +=nums[right];
            while ( sum >= target) {
                minLength = minLength == 0 ? right - left + 1 : Math.min(right - left + 1, minLength);
                sum -= nums[left++];
            }
            right++;
        }
        return minLength;
    }
}

前缀和

很巧妙的一个是利用了二分法，然后查询中间子数组的时候不变nums而变target，让newTarget = target + sums[i-1], newTarget就是从i-1开始查找的值，相当于从第一个元素开始查找的target。

还有注意到是当未查找到时候不能直接跳过，而需要继续进行比较。

-mid-1 可以用 ~mid取反操作代替。

我们只需要找到 sums[k]-sums[j]>=s，那么 k-j 就是满足的连续子数组，但不一定是最小的，所以我们要继续找，直到找到最小的为止。怎么找呢，我们可以使用两个 for 循环来枚举，但这又和第一种暴力求解一样了，所以我们可以换种思路，求 sums[k]-sums[j]>=s 我们可以求 sums[j]+s<=sums[k]，那这样就好办了，因为数组sums中的元素是递增的，也就是排序的，我们只需要求出 sum[j]+s 的值，然后使用二分法查找即可找到这个 k。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    // sums[i] : 0-i-1的前缀和,即前i个元素和
    // 
    public int minSubArrayLen(int target, int[] nums) {
        int n = nums.length;
        int[] sums = new int[n + 1];
        int sum = 0;
        int minLength = Integer.MAX_VALUE;
        for (int i = 1;i<= n; i++) {
            sums[i] = sums[i-1] + nums[i - 1];
        }
        for (int i = 1;i <=n; i++) {
            // 这里有个坑，不能用target累加，不然会重复加前面的和，应该用target+sums[i+1],taeget不变
            // target 加上 前i-1个和，然后进行二分查找target，用于计算中间区间
            int newTarget  = target + sums[i - 1];
            int mid = Arrays.binarySearch(sums, newTarget);
            // 未找到
            if (mid < 0) {
                // 没找到也不能直接跳过。 
                mid = -mid - 1;
            }
            // 找到target,区间长度：mid - (i-1); 即mid - i + 1。
            if (mid <= n)
            minLength = Math.min(minLength, mid - i + 1);
        }
        return minLength == Integer.MAX_VALUE ? 0 : minLength;
    }
}

17. LIS 无重复的最长连续子数组(滑动窗口板子)

image-20210727163626121 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int lengthOfLongestSubstring(String s) {
        if (s.length() == 0) {
            return 0;
        }

        int left = 0;
        int right = 0;
        int max = 0;
        Map<Character, Integer> map = new HashMap<>();
        while (right < s.length()) {
            char c = s.charAt(right);
            if (map.containsKey(c)) {
                left = Math.max(map.get(c) + 1, left);
            }
            map.put(c, right);
            max = Math.max(max, right - left + 1);
            right++;
        }
        return max;
    }
}

18. 二叉树的最近公共祖先

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null || p == null || q == null) {
            return null;
        }
        // 遇到p/q就返回
        if (root == p || root == q) {
            return root;
        }
        // left的返回值为p/q
        TreeNode left = lowestCommonAncestor(root.left, p , q);
        // right的返回值为p/q
        TreeNode right = lowestCommonAncestor(root.right, p, q);

        if(left != null && right != null) return root;
        if (left != null) return left;
        if (right != null) return right;
        return null;
    }
}

19 相交链表

1
2
3
4
5
6
7
8
9
10
11
12
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        if (headA == null || headB == null) return null;
        ListNode pA = headA;
        ListNode pB = headB;
        while (pA != pB) {
            pA = pA == null ? headB : pA.next;
            pB = pB == null ? headA : pB.next;
        }
        return pA;
    }
}

左神算法笔记

1。

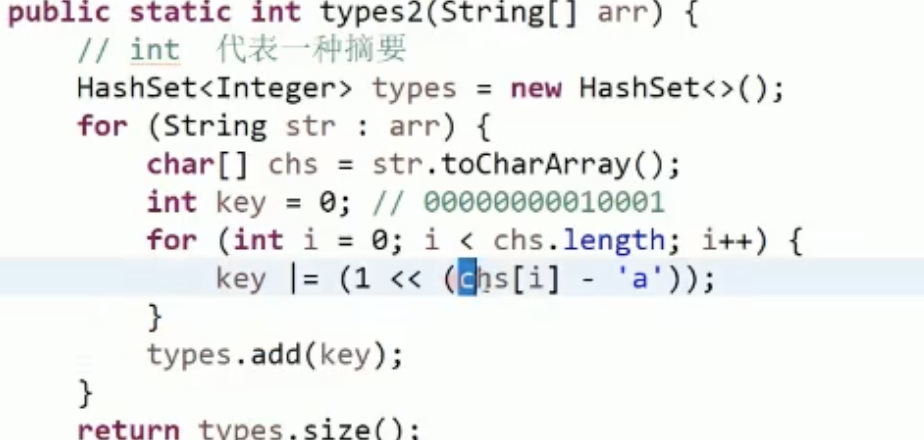
image-20210731094636587

a-z一共26个字符，所以首先可以想到用26位的boolean数组代表每个字符是否出现过。

再优化，可以将数组优化为位运算。

image-20210731094809098

key |= (1 << (chs[i] - 'a'))表示出现一个字符，那么key 进行或操作，可以将该字符的位置置为1，最后每出现的位置不一样代表一个不同的组合。相当于把数组优化成为位运算，int 32位替代boolean[]数组，0和1代表false和true。

同理如果表示小写字母a-zA-Z,可以用long类型进行代替，long类型64位，足够。

image-20210731102300531

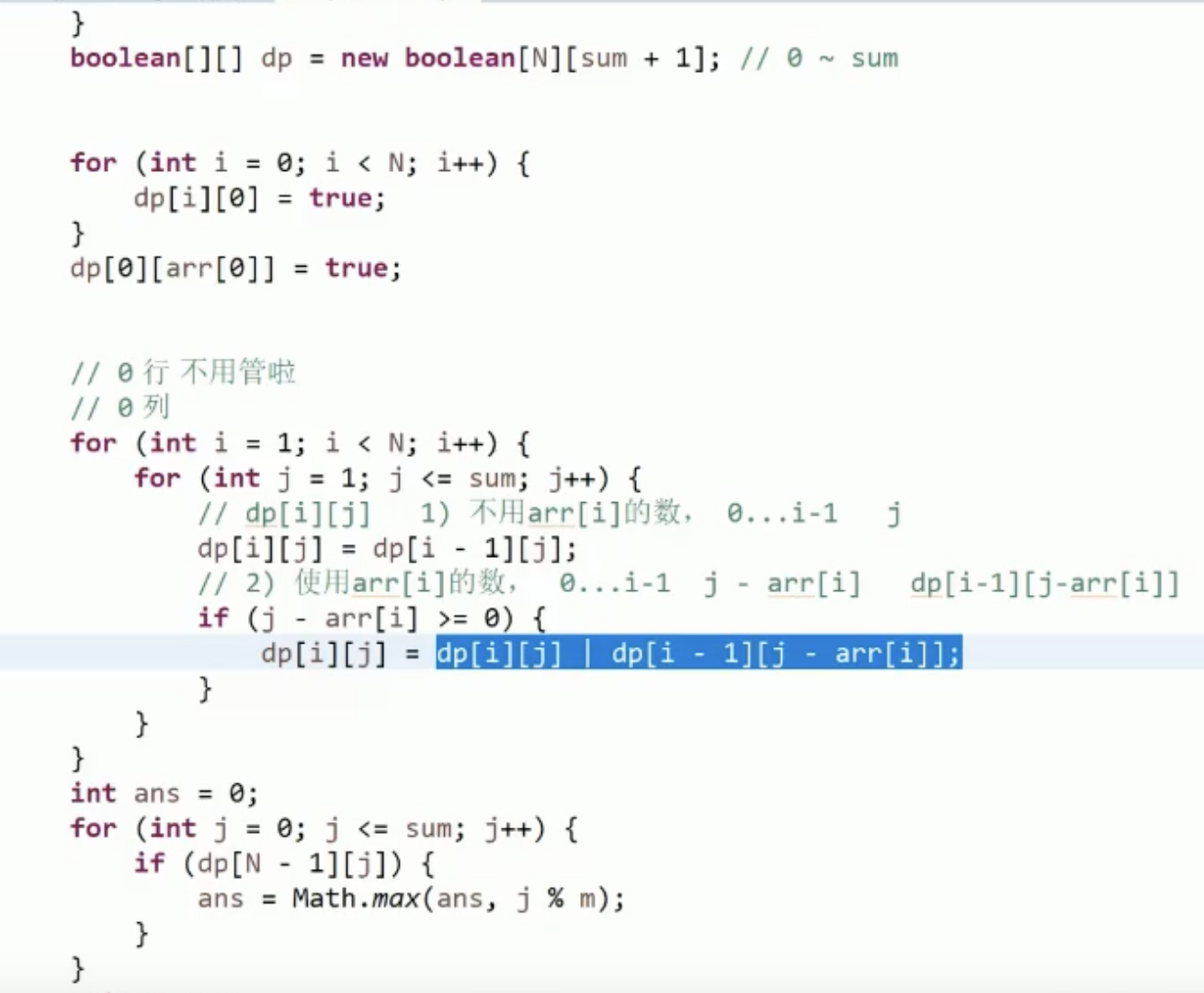
背包存在问题：

image-20210731101612484
image-20210731150053618

20.滑动窗口最大值（大根堆、单调队列、分块+预处理）

image-20210731160059157

一开始看错题意，求成了前i个最大的数字，使用了动态规划，有点尴尬。

暴力的话基本用例能过，但是后面会超时，时间复杂度是O（n^2）；

方法一：使用大根堆，存储一个二元组（这个存储方式很方便，学习了），先按num降序排列，然后按照idx降序排列。滑动窗口每次移动都新加一个元素，然后查看堆顶元素的索引是否在窗口内，如果不在就抛弃掉。时间复杂度O（nlogn）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {

    public int[] maxSlidingWindow(int[] nums, int k) {
        int n = nums.length;
        if (n == 1 || k == 1) return nums;
        // int[0] : num, int[1]:idx 先按num降序排列，然后按照idx降序排列
        PriorityQueue<int[]> queue = new PriorityQueue<>((o1,o2) -> 
            o2[0] != o1[0] ? o2[0] - o1[0] : o2[1] - o1[1]);
        int[] res = new int[n - k + 1];
        // 初始化前k个数入堆
        for(int i = 0; i < k; i++) {
            queue.offer(new int[] {nums[i], i});
        }
        res[0] = queue.peek()[0];
        // 依次入堆
        for (int i = 1; i < n - k + 1; i++) {
            queue.offer(new int[] {nums[i + k - 1], i + k -1});
            // 移除掉不属于窗口中的
            while (!queue.isEmpty() && queue.peek()[1] < i) {
                queue.poll();
                // System.out.println("i = "+ i +"时移除掉" +queue.poll()[0]);
            }
            // 剩下的就是属于窗口中最大的一个元素。注意不能是poll（）
            res[i] = queue.peek()[0];
        }
        return res;
    }

}

21.网络延迟时间（Dijkstra）

image-20210802160852717

主要学习Dijkstra算法，还可以使用优先队列优化，因为Dijkstra每次从未选择结点中距离最小的点开始，所以很适合使用小根堆进行存储。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
    public int networkDelayTime(int[][] times, int n, int k) {
        final int INF = Integer.MAX_VALUE / 2;
        int[][] g = new int[n][n];
        for (int i =0; i < n; i++) {
            Arrays.fill(g[i], INF);
        }
        // 初始化临接矩阵
        for (int[] t : times) {
            // 序号从0开始
            g[t[0] - 1][t[1] - 1] = t[2];
        }
        // 最短距离数组
        int dist[] = new int[n];
        Arrays.fill(dist, INF);
        // 由于从 k 开始，所以该点距离设为 0，也即源点
        dist[k - 1] = 0;
        // 是否访问过
        boolean[] visited = new boolean[n];

        // 最外层遍历每个结点
        for (int i = 0; i < n; i++) {
            // 记录中间结点
            int middle = -1;
            // 找未走过结点中距离最小的结点
            for (int j = 0; j < n; j++) {
                // 如果结点没有访问过，且 （中间结点暂时没有，或者有中间结点，但是直接到当前结点距离小于通过中间结点，更新为直接到达）
                if (!visited[j] && (middle == -1 || dist[j] < dist[middle])) {
                    middle = j;
                }
            }
            visited[middle] =true;

            // 用该点的距离更新后续结点
            for (int j = 0; j < n; j++) {
                dist[j] = Math.min(dist[j], dist[middle] + g[middle][j]);
            }
        }

        // 找距离最长的点
        int res = Arrays.stream(dist).max().getAsInt();
        return res == INF ? -1 : res;
    }
}

22.分割回文串

image-20210802165349851 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
    // 回溯+动态规划。动态规划快速判断是否是回文串，回溯进行全排列。
    // dp[i][j] = true, i>=j; dp[i+1][j-1] && s[i] == s[j]
    List<List<String>> res = new ArrayList<>();
    public List<List<String>> partition(String s) {
        int n = s.length();
        boolean[][] dp = new boolean[n][n];
        for (int i = 0; i < n; i++) {
            Arrays.fill(dp[i], true);
        }
        // 注意这里是从后往前，不然会出错。
        for (int i = n - 1; i >= 0; i--) {
            for (int j = i + 1; j < n; j++) {
                dp[i][j] = s.charAt(i) == s.charAt(j) && dp[i + 1][j - 1];
            }
        }

        backTrack(s,0,n,new LinkedList<String>(),dp);
        return res;
    }
        // i 表示当前左边的位置
    private void backTrack(String s, int i, int n,LinkedList<String> track, boolean[][] dp) {
        if (i == n) {
            res.add(new ArrayList<>(track));
            return;
        }
        for (int j = i; j < n; j++) {
          if (isHuiWen(dp,i,j)) {
              track.add(s.substring(i,j+1));
              backTrack(s, j+1,n,track,dp);
              track.removeLast();
          }
        }

    }

    public boolean isHuiWen(boolean[][] dp, int i, int j) {
        return dp[i][j];
    }
}

23.圆环回原点问题

圆环上有10个点，编号为0~9。从0点出发，每次可以逆时针和顺时针走一步，问走n步回到0点共有多少种走法。

本题考察的是动态规划。

如果你之前做过leetcode的70题爬楼梯，则应该比较容易理解这题的思路：走n步到0的方案数=走n-1步到1的方案数+走n-1步到9的方案数。 因此，若设dp[i][j]为从0点出发走i步到j点的方案数，则递推式为： image

ps: 公式之所以取余是因为j-1或j+1可能会超过圆环0~9的范围

参考代码

1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def backToOrigin(self,n):
        #点的个数为10
        length = 10
        dp = [[0 for i in range(length)] for j in range(n+1)]
        dp[0][0] = 1
        for i in range(1,n+1):
            for j in range(length):
                #dp[i][j]表示从0出发，走i步到j的方案数
                dp[i][j] = dp[i-1][(j-1+length)%length] + dp[i-1][(j+1)%length]
        return dp[n][0]

24.最长回文子串（动态规划）

image-20210809162416109

shopee一面，没怎么做出来，我和面试官思路不一样，导致面试官提示我修改的时候我一脸懵逼。

dp[i][j] = dp[i + 1][j - 1] && s[i] == s[j].表示从i到j的子串是不是回文串。

由于计算dp[i] 需要用到dp[i+1]. 所以选择从后往前遍历。

dp[i][j] = s.charAt(i) == s.charAt(j) && (j - i + 1< 3 || dp[i + 1][j - 1]);

在首尾相等的时候， j-i+1 <3 表示长度为3，去掉首位后为1，必然是回文串，dp[i + 1][j - 1] =true表示长度超过3，但是去掉首尾后也是回文串。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public String longestPalindrome(String s) {
        int n = s.length();
        String res = "";
        boolean[][] dp = new boolean[n][n];
        for (int i = n - 1; i >= 0; i--) {
            for (int j = i; j < n; j++) {
                dp[i][j] = s.charAt(i) == s.charAt(j) && (j - i < 2 || dp[i + 1][j - 1]); //j - i 代表长度减去 1        
              // 表示i到j是回文串，且长度比之前存储的最大回文串长度长，那么就更新
                if (dp[i][j] &&  j - i + 1 > res.length()) {
                    res = s.substring(i, j + 1);
                }
            }
        }
        return res;
    }
}

25.最长无重复子串（滑动窗口）

image-20210811210954661

快慢指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int lengthOfLongestSubstring(String s) {
        if (s.length() == 0) return 0;
        int left = 0;
        int right = 0;
        int res = 0;
      // key:char ,value:index
        Map<Character, Integer> map = new HashMap<>();
        map.put(s.charAt(0), 0);
        while (right < s.length()) {
            char c = s.charAt(right);
          // 这里比较妙。注意是用left进行比较，遇到重复的就到left下一位，如果遇到两个重复的如bnsdmf aa sdfs，那么在到第二个a时会直接让left指到第二个a。
            if (map.containsKey(c)) {
                left = Math.max(map.get(c) + 1, left);
            }
            map.put(c, right);
            res = Math.max(res, right - left + 1);
            right++;
        }
        return res;

    }
}

26.K个一组反转链表（迭代）

image-20210811223826336 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        if (head == null || head.next == null){
            return head;
        }
        ListNode dummy=new ListNode(0);
        dummy.next=head;
        //初始化pre和end都指向dummy。pre指每次要翻转的链表的头结点的上一个节点。end指每次要翻转的链表的尾节点
        ListNode pre=dummy;
        ListNode end=dummy;

        while(end.next!=null){
            //循环k次，找到需要翻转的链表的结尾,这里每次循环要判断end是否等于空,因为如果为空，end.next会报空指针异常。
            //dummy->1->2->3->4->5 若k为2，循环2次，end指向2
            for(int i=0;i<k&&end != null;i++){
                end=end.next;
            }
            //如果end==null，即需要翻转的链表的节点数小于k，不执行翻转。
            if(end==null){
                break;
            }
            //先记录下end.next,方便后面链接链表
            ListNode next=end.next;
            //然后断开链表
            end.next=null;
            //记录下要翻转链表的头节点
            ListNode start=pre.next;
            //翻转链表,pre.next指向翻转后的链表。1->2 变成2->1。 dummy->2->1
            pre.next=reverse(start);
            //翻转后头节点变到最后。通过.next把断开的链表重新链接。
            start.next=next;
            //将pre换成下次要翻转的链表的头结点的上一个节点。即start
            pre=start;
            //翻转结束，将end置为下次要翻转的链表的头结点的上一个节点。即start
            end=start;
        }
        return dummy.next;


    }
    //链表翻转
    // 例子：   head： 1->2->3->4
    public ListNode reverse(ListNode head) {
         //单链表为空或只有一个节点，直接返回原单链表
        if (head == null || head.next == null){
            return head;
        }
        //前一个节点指针
        ListNode preNode = null;
        //当前节点指针
        ListNode curNode = head;
        //下一个节点指针
        ListNode nextNode = null;
        while (curNode != null){
            nextNode = curNode.next;//nextNode 指向下一个节点,保存当前节点后面的链表。
            curNode.next=preNode;//将当前节点next域指向前一个节点   null<-1<-2<-3<-4
            preNode = curNode;//preNode 指针向后移动。preNode指向当前节点。
            curNode = nextNode;//curNode指针向后移动。下一个节点变成当前节点
        }
        return preNode;

    }


}

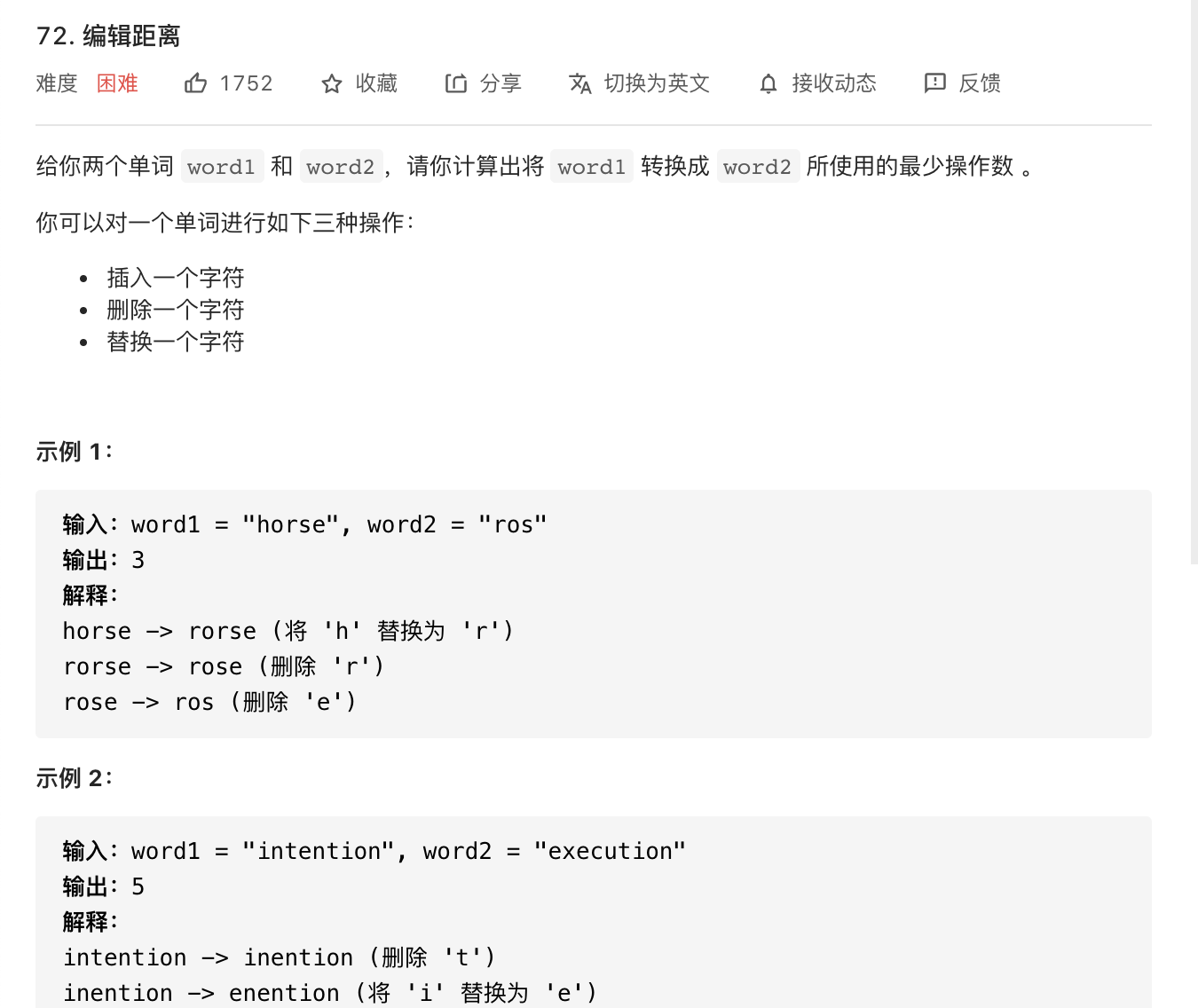
27.编辑距离*

image-20210812220723796

这道题比较难，但是是典型的动态规划。需要反复吃透。

要把一个单词变成另一个单词，先不考虑其他的，变成另一个单词前有哪几种状态？

题目提供了三种操作，那么最后也可以通过三种方式变换。

第一种，比word1少一个字符变为word2的步数+1，即只需要多删除一次。

第二种，word1变成word2少一位的步数+1，即只需要多插入一个。

第三种，word2变成和word2字符数一样的步数。分两种情况：最后一个字符相等，可以直接变换。不相等，多一次替换+1.

考虑初始化，任何空串到单词，和单词到空串，都需要删除或插入n次。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    // dp[i][j] : word1前i个字符到word2前j个字符的编辑距离
    // 情况一：删除一个字符 horse -> hors -> ros， dp[i - 1][j] + 1
    // 情况二：插入一个字符 horse -> ro -> ros ,到少一位+1次，dp[i][j - 1] + 1
    // 情况三：替换一个字符 horse -> roe -> ros,到相等位替换一次,分为最后一个字符是否相等。
    //.       s[i] == s[j] : dp[i-1][j-1], s[i] != s[j],替换一次,dp[i-1][j-1] + 1;
    public int minDistance(String word1, String word2) {
        int m = word1.length();
        int n = word2.length();

        int[][] dp =new int[m + 1][n + 1];
        // 初始化dp
        for (int i = 0; i <= n; i++ ) {
            dp[0][i] = i;
        }
        for (int j = 0; j <= m; j++) {
            dp[j][0] = j;
        }

        for (int i =1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
              // 先写dp方程，发现最后dp[i - 1][j -1]有两种情况，于是再进行判断。
              // 取上面三种情况的最小值，三个数进行比较用两次Math.min.
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = Math.min(Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1), dp[i - 1][j -1]);
                    } else {
                      dp[i][j] = Math.min(Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1), dp[i - 1][j -1] + 1);  
                    }

            }
        }

        return dp[m][n];
    }
}

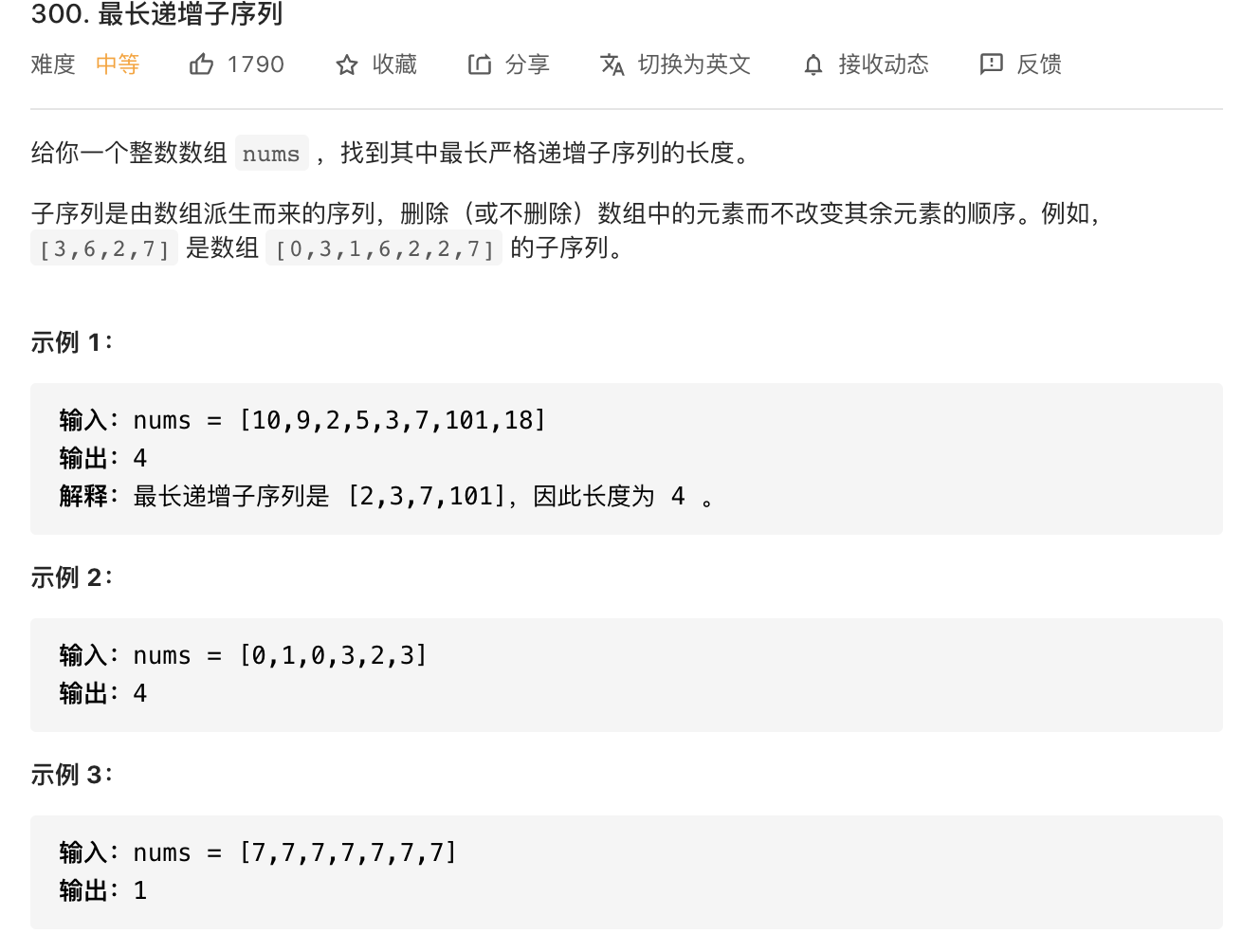
28.最长自增子序列（动态规划）

image-20210812232230313 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    // dp[i] : 0-i 递增子序列长度，包括i。
    // dp[i] = Math.max(dp[i], dp[j] + 1)
    public int lengthOfLIS(int[] nums) {
        int n = nums.length;
        if (n <= 0) return 0;

        int[] dp = new int[n];

        Arrays.fill(dp, 1);

        // 外层i表示循环到第i个字符
        int res = 1;
        for (int i = 1; i < n; i++) {
            // 内层j表示从0-i找nums[i]为结尾的最长递增子序列长度
            for (int j = 0; j < i; j++) {
                // 找到一个比nums[i]小的
                if ( nums[j] < nums[i]) {
                    // 填入第i个字符结尾的最长长度
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
                res = Math.max(res, dp[i]);
            }
        }
        return res;
    }
}

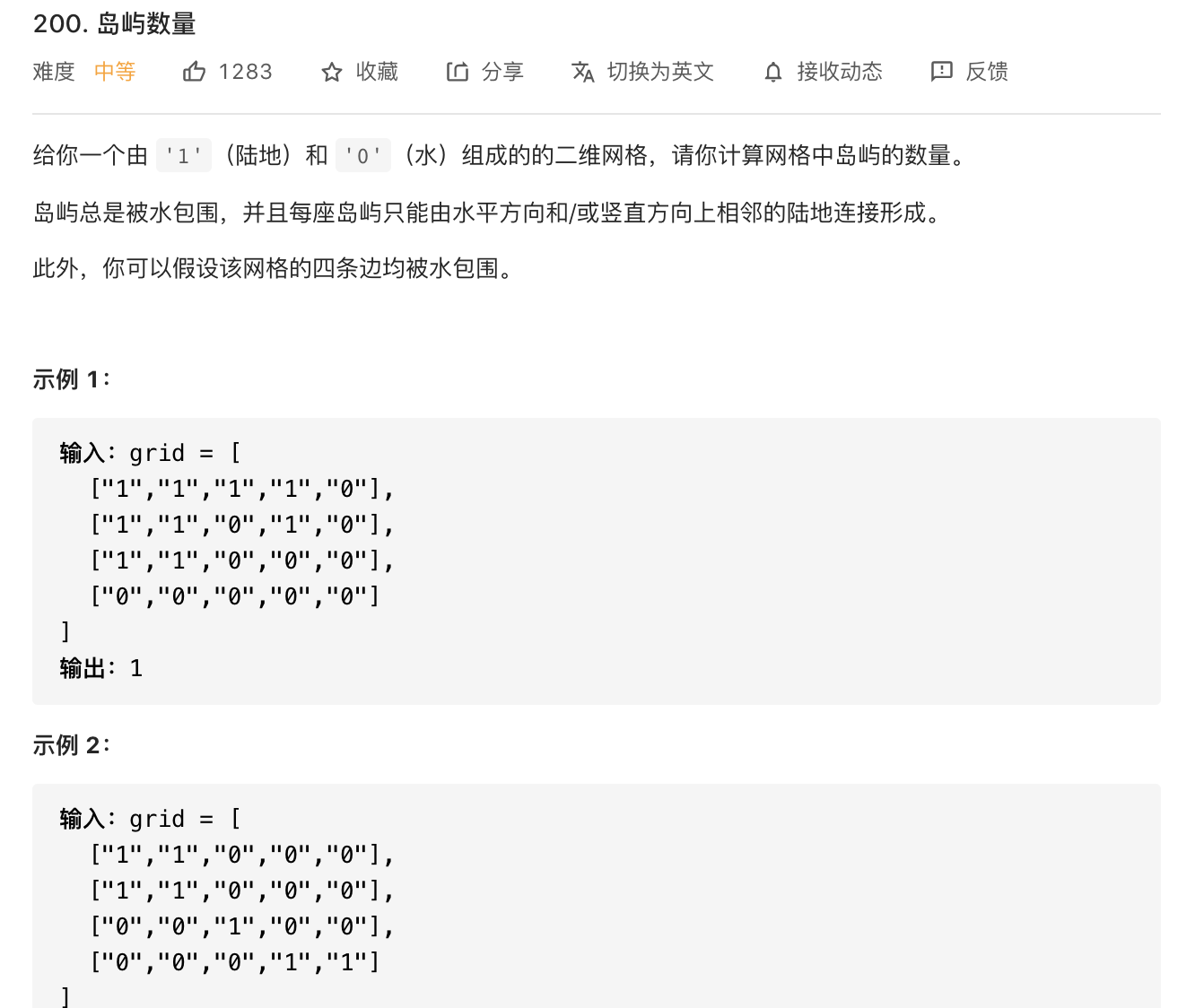
29.岛屿数量（DFS、并查集）

image-20210816225054217 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
    int m;
    int n;
    public int numIslands(char[][] grid) {
        m = grid.length;
        n = grid[0].length;
        int res = 0;
        // 依次循环
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                // 发现一个岛屿
                if (grid[i][j] == '1') {
                    infect(grid, i ,j);
                    res++;
                }
            }
        }
        return res;
    }

    // 感染函数，DFS，把所有相连的1都修改为2
    public void infect(char[][] grid, int i, int j) {
        if (i < 0 || i >= m || j < 0 || j >= n ||  grid[i][j] != '1')  {
            return;
        }
        if (grid[i][j] == '1') {
            grid[i][j] = '2';
        }
        infect(grid, i + 1, j);
        infect(grid, i, j + 1);
        infect(grid, i - 1, j);
        infect(grid, i, j - 1);
    }
}

DFS的方法比较简单，主要学习并查集的方式。

并查集：并查集是一种树型的数据结构，用于处理一些不交集（Disjoint Sets）的合并及查询问题。

特点：孩子节点保存父节点的指针。

无向图中（上图二维矩阵就可以看作一个无向图），如果两个元素有关联，那么将一个作为根节点，然后将其他元素指向根节点，如果两个元素连通，那么他们的最祖先的结点一定是一样的。可以进行聚类。

在并查集中，每个集合的代表即是集合的根节点。

  • “查找”根据其父节点的引用向根行进直到到底树根。
  • “联合”将两棵树合并到一起，这通过将一棵树的根连接到另一棵树的根。

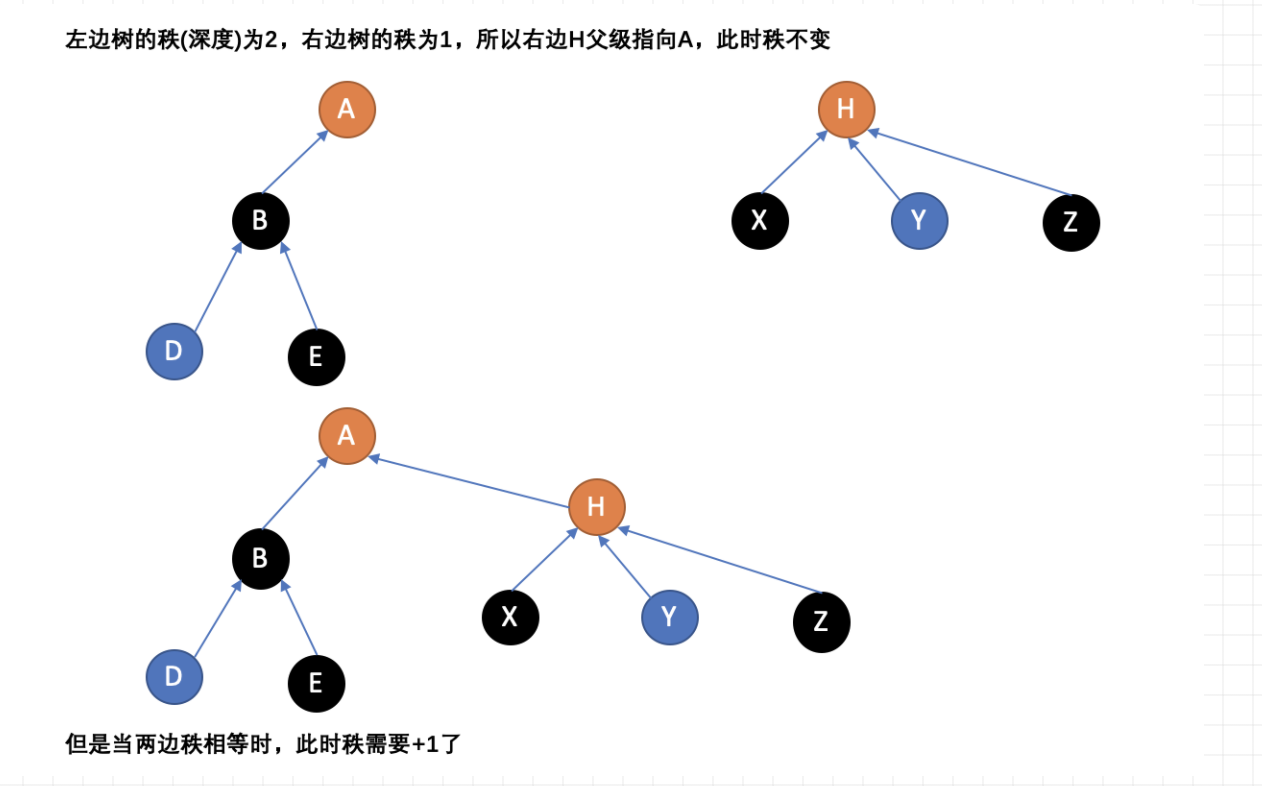
但是树可能不平衡，退化成链表。有两种优化方法：

1.按秩合并（按深度合并）：总是将更小的树连接至更大的树。单元素的树的秩定义为0，当两棵秩同为r的树联合时，它们的秩r+1。只使用这个方法将使最坏的运行时间提高至每个MakeSet、Union或Find操作

image-20210816225930951

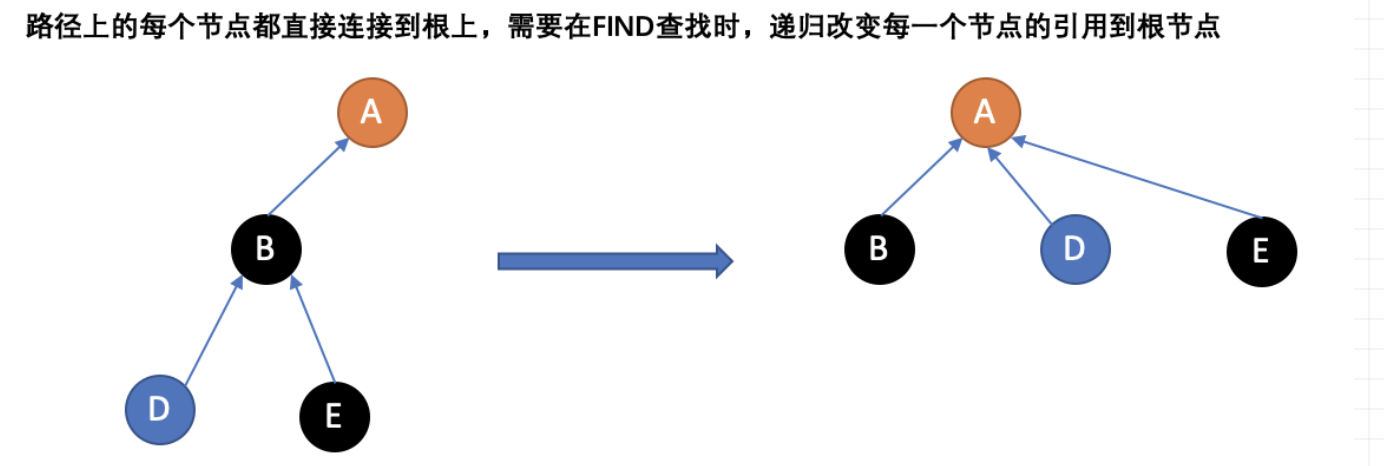
2.路径压缩。是一种在执行“查找”时扁平化树结构的方法。关键在于在路径上的每个节点都可以直接连接到根上

即把所有的孩子节点都连到最祖先节点上，树就变得很扁平化。

image-20210816230030139

30.三数之和（双指针）

image-20210818180147658

最开始想的是哈希表法，但是主要的点是去重，去重不方便。

既然寻找和为0，思路即遍历i，在i后面数组寻找和为 -nums[i]的组合。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
    List<List<Integer>> res = new ArrayList<>();
    public List<List<Integer>> threeSum(int[] nums) {
        int n = nums.length;
        if (n <= 0) return new ArrayList();
        Arrays.sort(nums);
        for (int i = 0; i < n - 2; i++) {
            // 去重，如[1,1]，跳过1；
            if (i > 0 && nums[i] == nums[i - 1]);
            if (nums[i] > 0) break;
            // 分解为在i后面的数组找和为 -nums[i]的数。双指针法
            int j = i + 1;
            int k = n - 1;
            int sum = nums[j] + nums[k];
            // 保证不交替寻找
            while (j < k) {
                if (sum == - nums[i]) {
                List<Integer> temp = new ArrayList<>();
                temp.add(nums[i]);
                temp.add(nums[j]);
                temp.add(nums[k]);
                res.add(temp);
                // 去重，k前一个和当前一样则直接跳过
                while (j < k && nums[k] == nums[k - 1]) {
                    k--;
                }
                // 去重
                while (j < k && nums[j] == nums[j + 1]) {
                    j++;
                }
                // 到达最后一个相同的数，继续寻找
                    j++;
                    k--;
                }else if ( sum > - nums[i]) {
                    k--;
                }else {
                    j++;
                }
            }

        }
        return res;
    }
}

31. 计算带精度的开方（二分）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int mySqrt(int x) {
        if (x == 1) return 1;
        double left = 1;
        double right = x;
        double newMid = 0.0;
        double mid = (left + right) / 2 ;
        System.out.println(mid);
      // 0.0001即精度，不断地逼近mid和newMid
        while (left < right && Math.abs(newMid - mid) > 0.00001) {
            if (mid  > x / mid) {
                right = mid;
            }else {
                left = mid;
            }
            newMid = mid;
            mid = (left + right) / 2 ;
        }
        System.out.println(mid);
        return (int)mid;
    }
}

32.搜索旋转排序数组

image-20210819161536022

二分法，虽然二分后一边不一定是有序数组，如 4 5 6， 7 1 2 3.但是 4 5 6是有序的，按照同样的思路再二分 7 1 2 3，得到 2 3是有序的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
    public int search(int[] nums, int target) {
        int n = nums.length;
        if (n <= 0) {
            return -1;
        }
        if (n == 1 && nums[0] == target) {
            return 0;
        }
        int left = 0;
        int right = n - 1;
        while (left <= right) {
            int mid = (left + right) / 2;
            if (nums[mid] == target) {
                return mid;
            }
            // 0-mid是有序数组
            if (nums[0] <= nums[mid]) {
                // target 位于0-mid之间，那么在0-mid中搜索
                if (nums[0] <= target && target < nums[mid]) {
                    right = mid -1;
                    // 否则在mid + 1- r中搜索
                }else {
                    left = mid + 1;
                }
                // 0 - mid 不是有序数组，如5 6 7 1 2 3 4，nums[mid] = 1
            } else {
                // 如果target处于mid - （n - 1）中，即 1 2 3 4中
                if (nums[mid] < target && target <= nums[n - 1]) {
                    left = mid + 1;
                }else {
                    right = mid - 1;
                }
            }
        }


        return -1;
    }
}

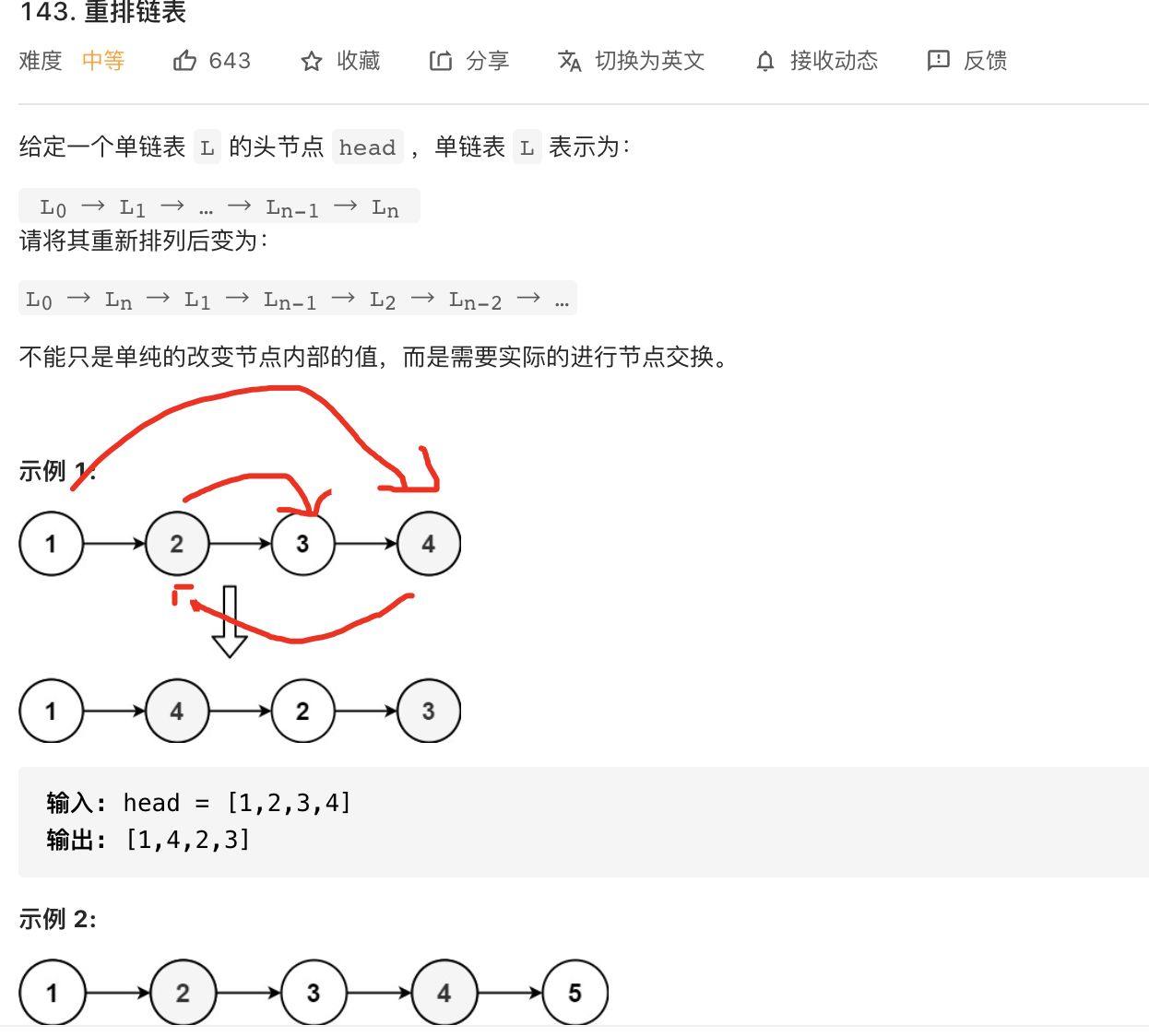
33.重排链表

image-20210819214009607

如图所示重排链表，类似一个环。

我的想法是把所有节点都存在list中，然后一次循环遍历i到 n /2，根据索引来修改指针。

比较繁琐，而且需要消耗O(n)的空间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public void reorderList(ListNode head) {
        List<ListNode> list = new ArrayList<>();

        ListNode cur = head;
        while (cur != null) {
            list.add(cur);
            cur = cur.next;
        }

        cur = head;
        int n =list.size();
      // 循环修改链表指针
        for (int i = 1; i <= n / 2; i++) {
          // 一次循环里操作两次,先指到后面的节点，再指到前面的节点
            cur.next = list.get(n - i);
            cur = cur.next;
          // 注意每次指向修改完成后把next 域置为null，不然会产生环
            cur.next = null;
          // 如果是偶数个防止中间两个相互连接形成环
            if (i != n / 2) {
                cur.next = list.get(i);
                cur = cur.next;
                cur.next = null;
            }
        }
      // 如果是奇数个最后再连接上中间的节点
        if ( n % 2 != 0) {
            cur.next = list.get(n / 2);
            cur = cur.next;
            cur.next = null;
        }

    }
}

优秀解法：不借助辅助空间。由于需要将前半段和后半段进行依次插入，所以先使用快慢指针找到链表的中点，分成两个链表，然后反转后半段链表，最后按次序合并两个链表。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public void reorderList(ListNode head) {
        ListNode midNode = getMidNode(head);
        ListNode l2 = midNode.next;
        midNode.next = null;
        ListNode lastHead = reverse(l2);
        merge(head, lastHead);
    }

        // 获取中点
    public ListNode getMidNode(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;
        while (fast.next != null && fast.next.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }
        return slow;
    }

      // 反转后半段
    public ListNode reverse(ListNode head) {
        ListNode pre = null, cur = head;
        while(cur != null){
            ListNode nxt = cur.next;
            cur.next = pre;
            pre = cur;
            cur = nxt;
        }
        return pre;
     }
        // 合并链表
     public void merge(ListNode l1, ListNode l2) {
         ListNode cur1 = l1;
         ListNode cur2 = l2;
         while (cur1 != null && cur2 != null) {
             cur1 = l1.next;
             cur2 = l2.next;

             l1.next = l2;
             l1 = cur1;

             l2.next = l1;
             l2 = cur2;
        }
     }
}

34.螺旋矩阵（技巧）

image-20210819230301483

分层地去遍历，先遍历外圈，再缩小遍历第二圈。

使用四个界限来表示上下左右

image-20210819230428531 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        int left = 0, right = n - 1;
        int top = 0, down = m - 1;
        List<Integer> res = new ArrayList<>();

        while (true) {
            // 遍历顶层，top下移
            for (int i = left; i <= right; i++) {
                res.add(matrix[top][i]);
            }
            top++;
            if (top > down) break;
            // 遍历右层
            for (int i = top; i <= down; i++) {
                res.add(matrix[i][right]);
            }
            right--;
            if (left > right) break;
            // 遍历下层,注意这里从右往左
            for (int i = right; i >= left; i--) {
                res.add(matrix[down][i]);
            }
            down--;
            if (top > down) break;
            // 遍历左层，注意这里从下往上
            for (int i = down; i >= top; i--) {
                res.add(matrix[i][left]);
            }
            left++;
            if (left > right) break;
        }
        return res;
    }

}

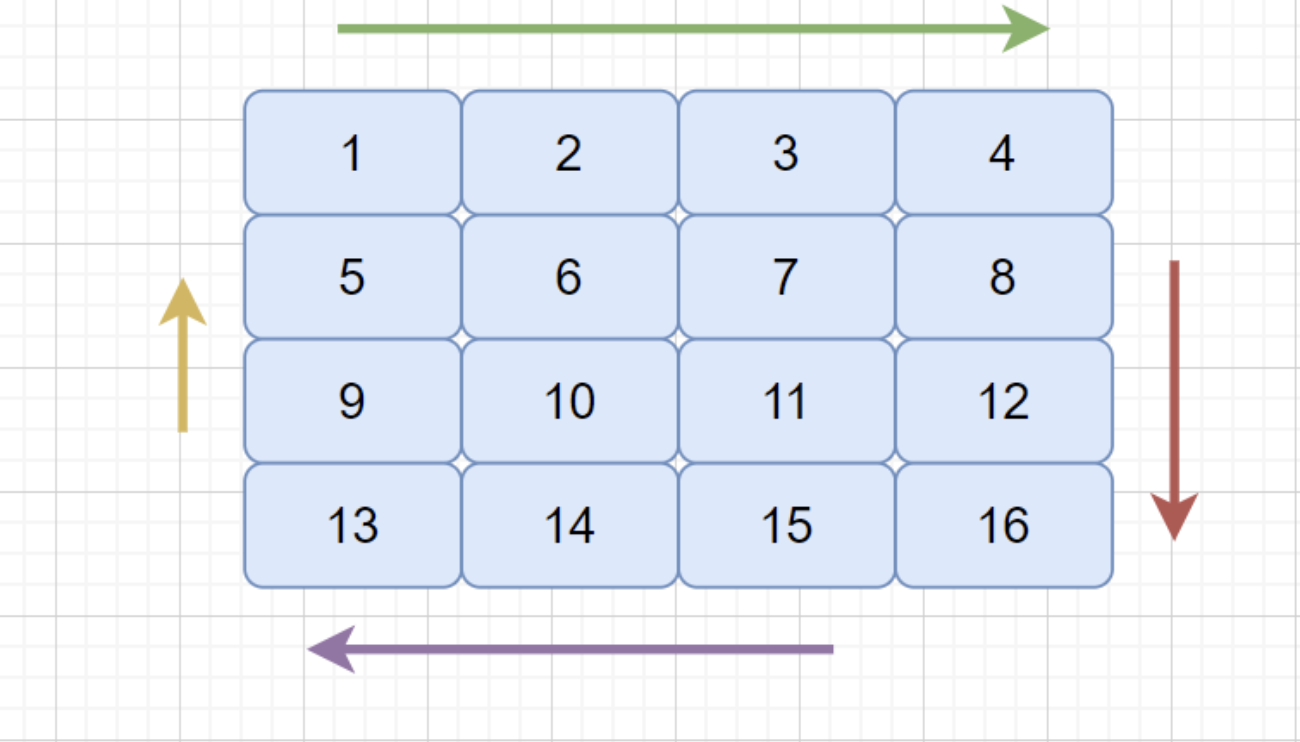
35.合并区间（排序）

image-20210821150518096

思路即按照数组第一维进行排序，然后判断当前数组第一位与前一数组最后一位的关系，如果可以合并，再看当前数组第二位和当前最大end的关系。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public int[][] merge(int[][] intervals) {
        int m = intervals.length;
        int n = intervals[0].length;
        if (m == 0) return null;
        Arrays.sort(intervals, (o1, o2) -> o1[0] - o2[0]);
        // start和end记录当前最大区间的起止
        int start = intervals[0][0];
        int end = intervals[0][1];
        List<int[]> list = new ArrayList<>();
        int k = 0;
        for (int i = 1; i < m; i++) {
            // [1,3][2,4]->[1,4] 区间增大
            if (intervals[i][0] <= end && intervals[i][1] > end) {
                end = intervals[i][1];
            }else if (intervals[i][0] > end){
                // [1,3][4,5],区间断层时，将上一次的结果保存
               list.add(new int[]{start, end});
               start = intervals[i][0];
               end = intervals[i][1];
            }
        }
        // 保存最后一个结果
        list.add(new int[]{start, end});
        return list.toArray(new int[list.size()][]);
    }
}

36.寻找峰值

https://leetcode-cn.com/problems/find-peak-element/

image-20210821151156181 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public int findPeakElement(int[] nums) {
        if(nums.length==1) return 0;
        int l=0,r=nums.length-1; 
        while(l<r){// [l,r] 型二分法,此处判别是开还是闭看l和r的取值
            int mid=(l+r)/2; // 向下取整,所以mid+1不会溢出
            if(nums[mid]>nums[mid+1]){// mid比右侧大, 峰顶在左侧或就在mid处
                r=mid;// [l,mid]
            }else if(nums[mid]<nums[mid+1]){
                l=mid+1;// mid比右侧小,峰顶在右侧[mid+1,r]
            }
        }// 退出循环时 l==r

        // 在l==r时,其实是没有判断当前是否就是答案, 但本题一定会有答案
        // ==>所以就没有去判断了
        return l; 
    }

}

37.二叉树最近公共祖先（递归）

https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree/

image-20210821152325594 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null || p == null || q == null) {
            return null;
        }
        if (root == p || root == q) {
            return root;
        }
        TreeNode left = lowestCommonAncestor(root.left,p, q);
        TreeNode right = lowestCommonAncestor(root.right,p , q);
        if (left != null && right != null) return root;
        if (left != null) return left;
        if (right != null) return right;
        return null;
    }
}

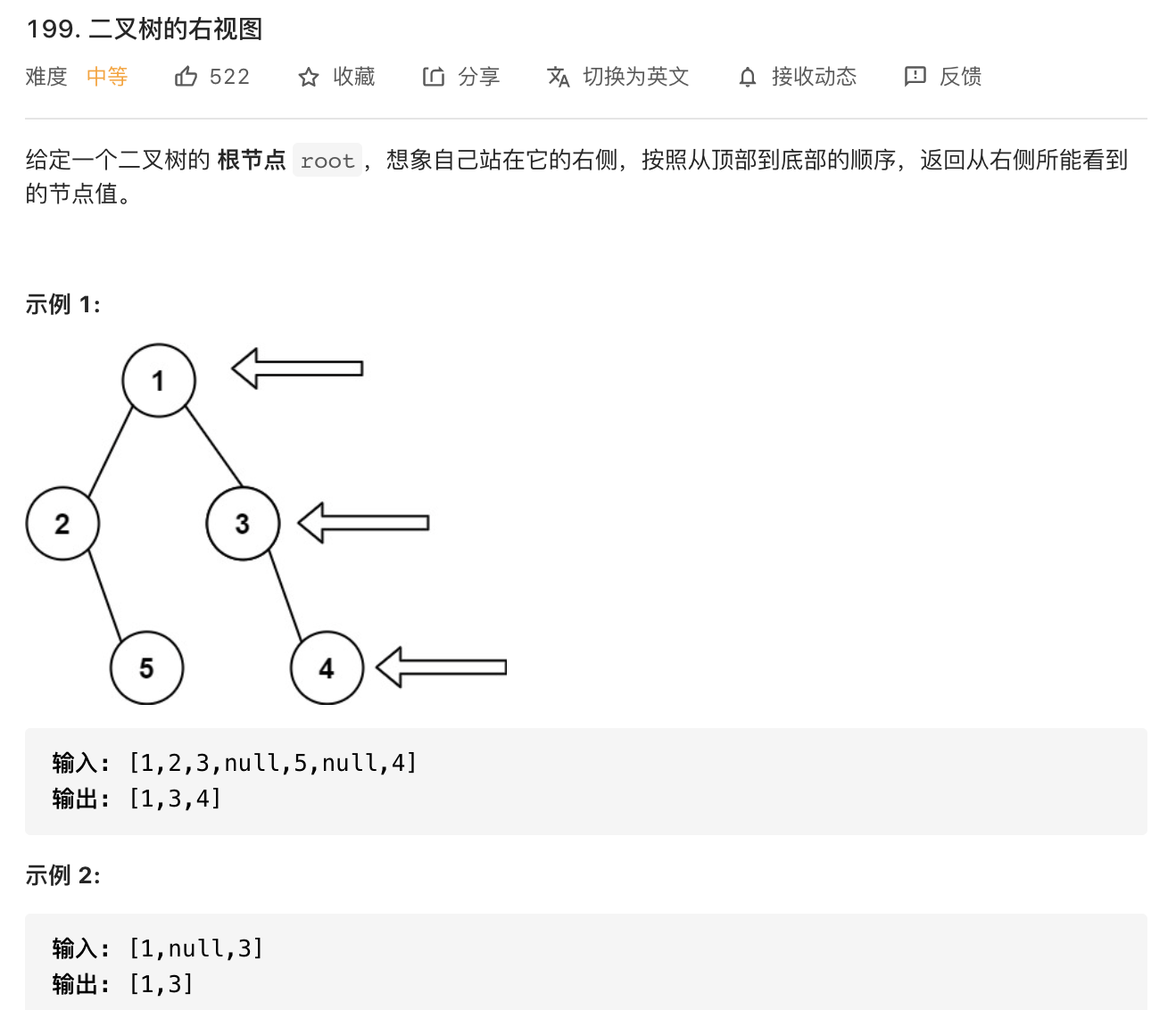
38.二叉树的右视图（层序遍历）

https://leetcode-cn.com/problems/binary-tree-right-side-view/

image-20210822183850014

最开始是想dfs进行递归右子树，然后提交后发现如果左子树比右子树深的话，左子树下面的部分也应该看得到，就进行不下去了。

后来看到评论说层序遍历，每次把最后一个元素添加即可。看到后恍然大悟的感觉，感觉很妙，思维转化能力非常重要。顺便回顾层序遍历的代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List<Integer> res = new ArrayList<>();
    public List<Integer> rightSideView(TreeNode root) {
        if (root == null) {
            return res;
        }
        order(root);
        return res;

    }

    public void order(TreeNode root) {
        Queue<TreeNode> q = new LinkedList<>();
        q.offer(root);
        while (!q.isEmpty()) {
          // level记录每层的节点
            List<Integer> level = new ArrayList<>();
          // 每次会把当前q中所有节点遍历记录下来，curSize相当于队列大小的快照，后面添加的都不会遍历。
            int curSize = q.size();
            for (int i = 0; i < curSize; i++) {
                TreeNode temp = q.poll();
                level.add(temp.val);
              // 对当前层每个节点遍历，如果有左右子树就添加到队列中，等待下次被遍历
                if (temp.left != null) {
                    q.offer(temp.left);
                } 
                if (temp.right != null) {
                    q.offer(temp.right);
                }
            }
          // 把每层最后一个节点添加到res
            res.add(level.get(level.size() - 1));
        }
    }
}

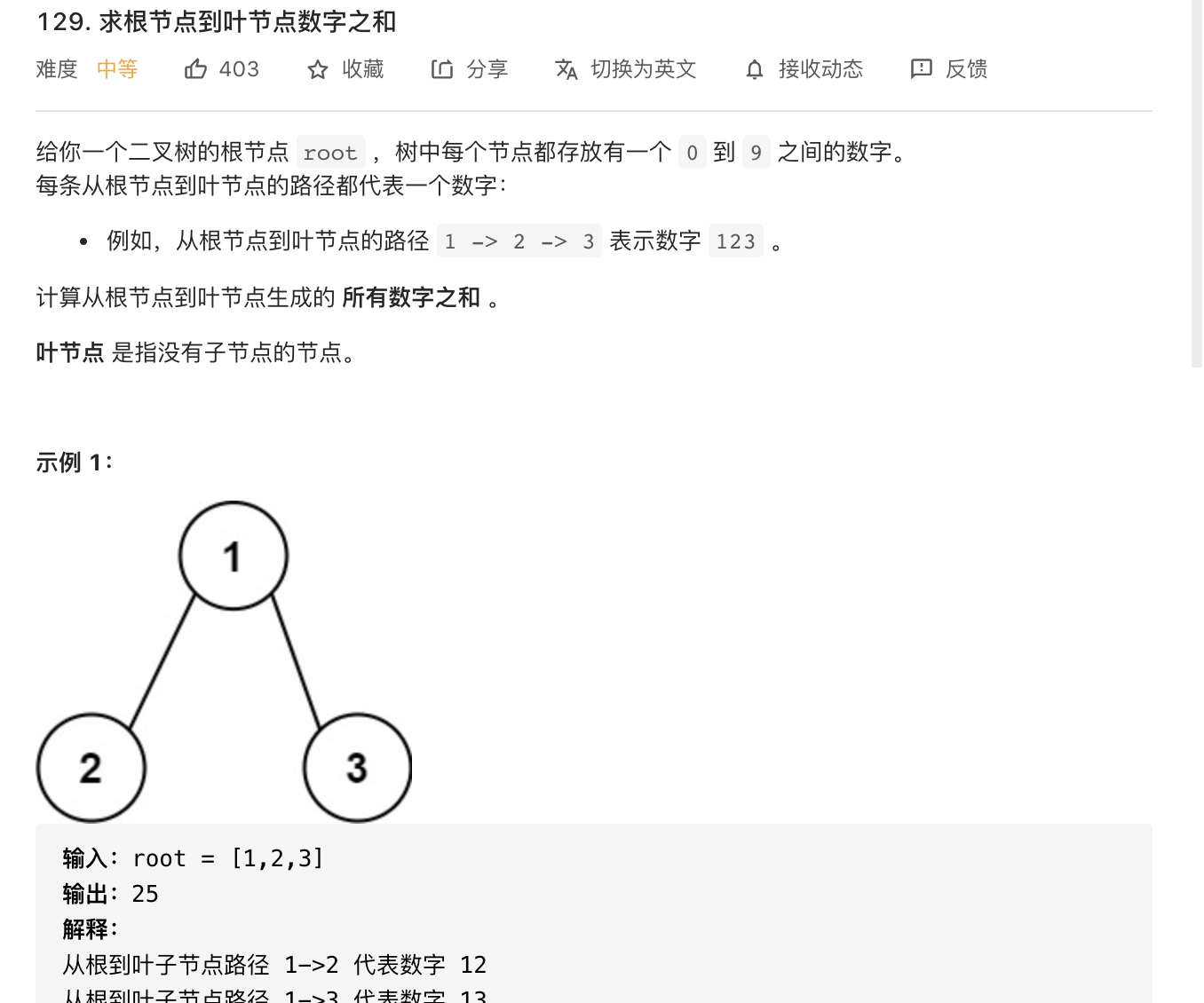
39.求根节点到叶子结点数字之和（递归）

https://leetcode-cn.com/problems/sum-root-to-leaf-numbers/

image-20210822213022299

dfs递归，判断当为叶子结点的时候加到sum上。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    int sum = 0;
    public int sumNumbers(TreeNode root) {
        dfs(root,0);
        return sum;
    }
    public void dfs(TreeNode root, int curNum) {
        if (root == null) {
            return;
        }
      // 到达叶子结点
        if (root.left == null && root.right == null) {
            sum += curNum * 10 + root.val;
        }
      // 每一层*10再相加
        dfs(root.left, curNum * 10 + root.val);
        dfs(root.right ,curNum * 10 + root.val);
    }
}

40.对角线遍历（规律技巧）

https://leetcode-cn.com/problems/diagonal-traverse/

image-20210822221741586

方法比较笨拙，即进行循环，先右走一步，再一直往坐下走，再下走一步，再一直往右上走，如果遇到右边界则往下走一步，遇到下边界则往右走一步。提交后只击败了9%

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class Solution {
    // 0,0 0,1 1,0 2,0 1,1 0,2 1,2 2,1 2,2
    // m = 3, n =3
    // 往左走一步，j+1. 然后j--直到0，往下走一步，然后i--j++直到i=0或j=n-1，如果j = n-1，i++；
    public int[] findDiagonalOrder(int[][] mat) {
        int m = mat.length;
        int n = mat[0].length;
        if (m == 0 || n == 0) {
            return new int[0];
        }
        int[] res= new int[m * n];
        int idx = 0;
        int i = 0, j = 0;
        res[idx] = mat[i][j];
        idx++;
        while (true) {
            if (i == m -1 && j == n -1) {
                break;
            }
            // 右走一步，到达右边界向下走
            if (i < m -1 && j == n - 1) {
                System.out.println(i + " " + j);
                i++;
                res[idx] = mat[i][j];
                idx++;
            }
            if (j < n - 1) {
                j++;
                res[idx] = mat[i][j];
                idx++;
            }
            // 左下走
            while (i < m - 1 && j > 0) {
                j--;
                i++;
                res[idx] = mat[i][j];
                idx++;
            }
            // 下走一步,遇到左边界向右走
            if (j < n -1 && i == m - 1) {
                j++;
                res[idx] = mat[i][j];
                idx++;
            }
            if (i < m - 1) {
                i++;
                res[idx] = mat[i][j];
                idx++;
            }
            // 往上走
            while (i > 0 && j < n - 1) {
                i--;
                j++;
                res[idx] = mat[i][j];
                idx++;
                System.out.println(i + " " + j);
            }
        }
        return res;
    }
}

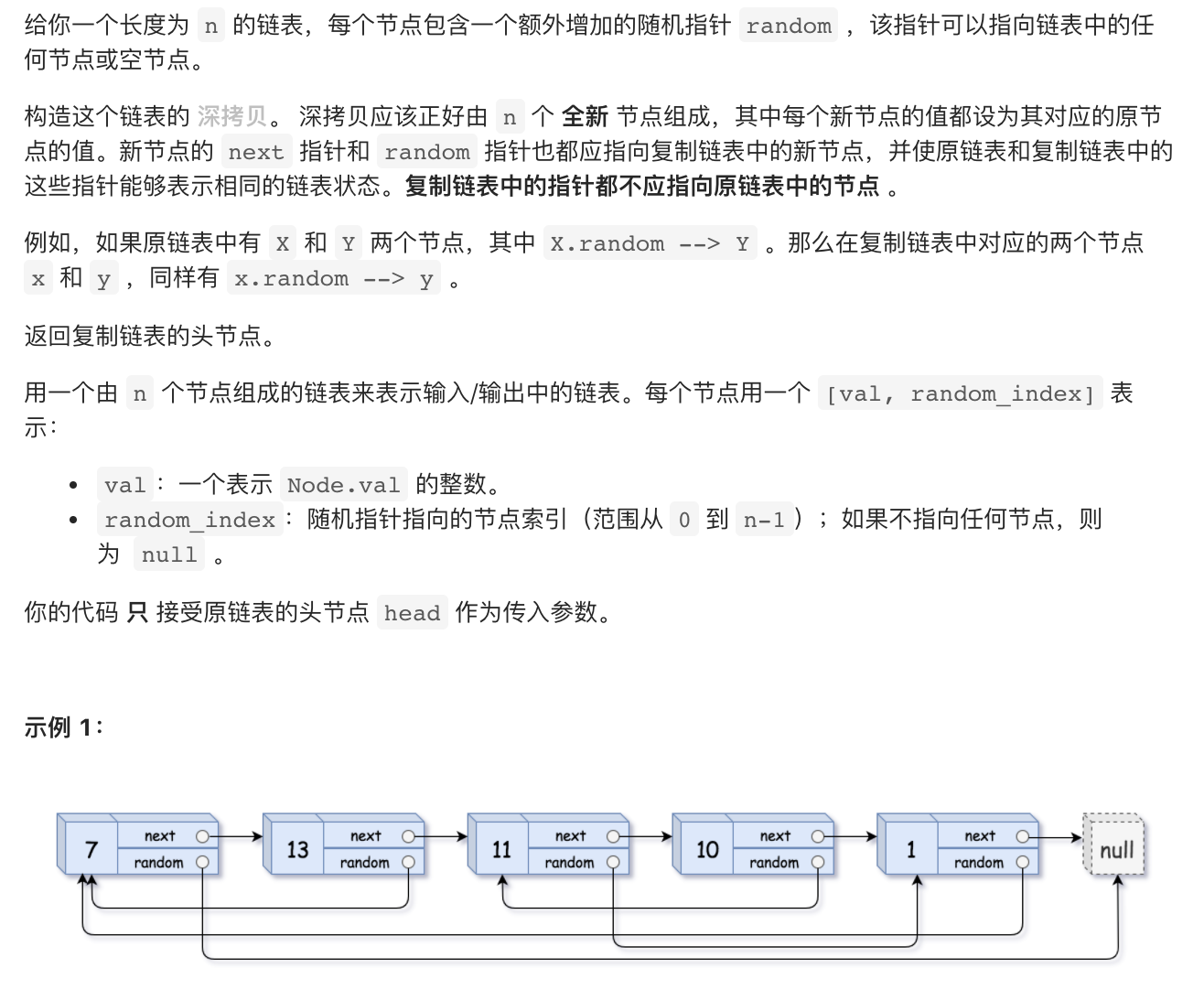
41.复制带随机指针的链表（哈希表）

https://leetcode-cn.com/problems/copy-list-with-random-pointer/

image-20210822231643557

题目意思即给一个单向链表，但是多了一个random指针，我们需要重新创建一个相同的单链表，每个节点都是新的节点，并且指向和原来保持一致。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
/*
// Definition for a Node.
class Node {
    int val;
    Node next;
    Node random;

    public Node(int val) {
        this.val = val;
        this.next = null;
        this.random = null;
    }
}
*/

class Solution {
    public Node copyRandomList(Node head) {
        Map<Node, Node> map = new HashMap<>();
      // 哨兵节点
        Node dummy = new Node(0);
      // 原链表的遍历指针
        Node oldCur = head;
      // 新链表的遍历指针
        Node newCur = dummy;
      // 先将链表连成单链表，map存储（原节点，新节点）
        while (oldCur != null) {

            // 新结点
            Node temp = new Node(oldCur.val);
            map.put(oldCur, temp);
            newCur.next = temp;
            newCur = newCur.next;
            oldCur = oldCur.next;
        }
      // 重置指针
        oldCur = head;
        newCur = dummy.next;
      // 设置随机指针
        while (oldCur != null) {
            Node node = map.get(oldCur.random);
            if (node != null) {
                newCur.random = node;

            }else {
                newCur.random = null;
            }
            newCur = newCur.next;
            oldCur = oldCur.next;
        }
        return dummy.next;
    }
}

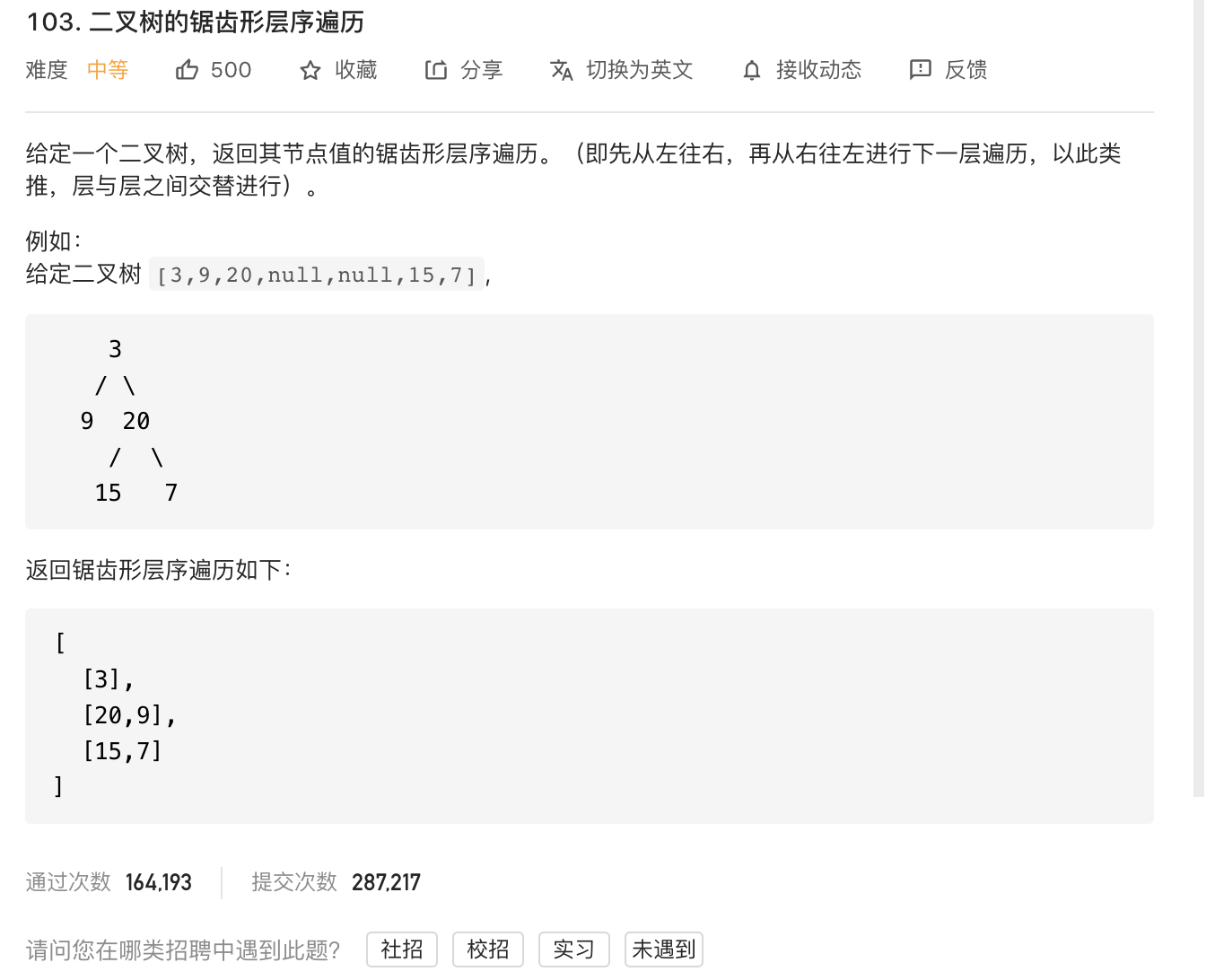
42. 二叉树锯齿层序遍历

https://leetcode-cn.com/problems/binary-tree-zigzag-level-order-traversal/

image-20210823155318167

isOrderLeft控制加到双端队列的头部还是尾部。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
        List<List<Integer>> ans = new LinkedList<List<Integer>>();
        if (root == null) {
            return ans;
        }

        Queue<TreeNode> q = new LinkedList<TreeNode>();
        q.offer(root);
        boolean isOrderLeft = true;

        while (!q.isEmpty()) {
            Deque<Integer> list = new LinkedList<Integer>();
            int size = q.size();
            for (int i = 0; i < size; ++i) {
                TreeNode curNode = q.poll();
                if (isOrderLeft) {
                    list.offerLast(curNode.val);
                } else {
                    list.offerFirst(curNode.val);
                }
                if (curNode.left != null) {
                    q.offer(curNode.left);
                }
                if (curNode.right != null) {
                    q.offer(curNode.right);
                }
            }
            ans.add(new LinkedList<Integer>(list));
            isOrderLeft = !isOrderLeft;
        }

        return ans;
    }
}

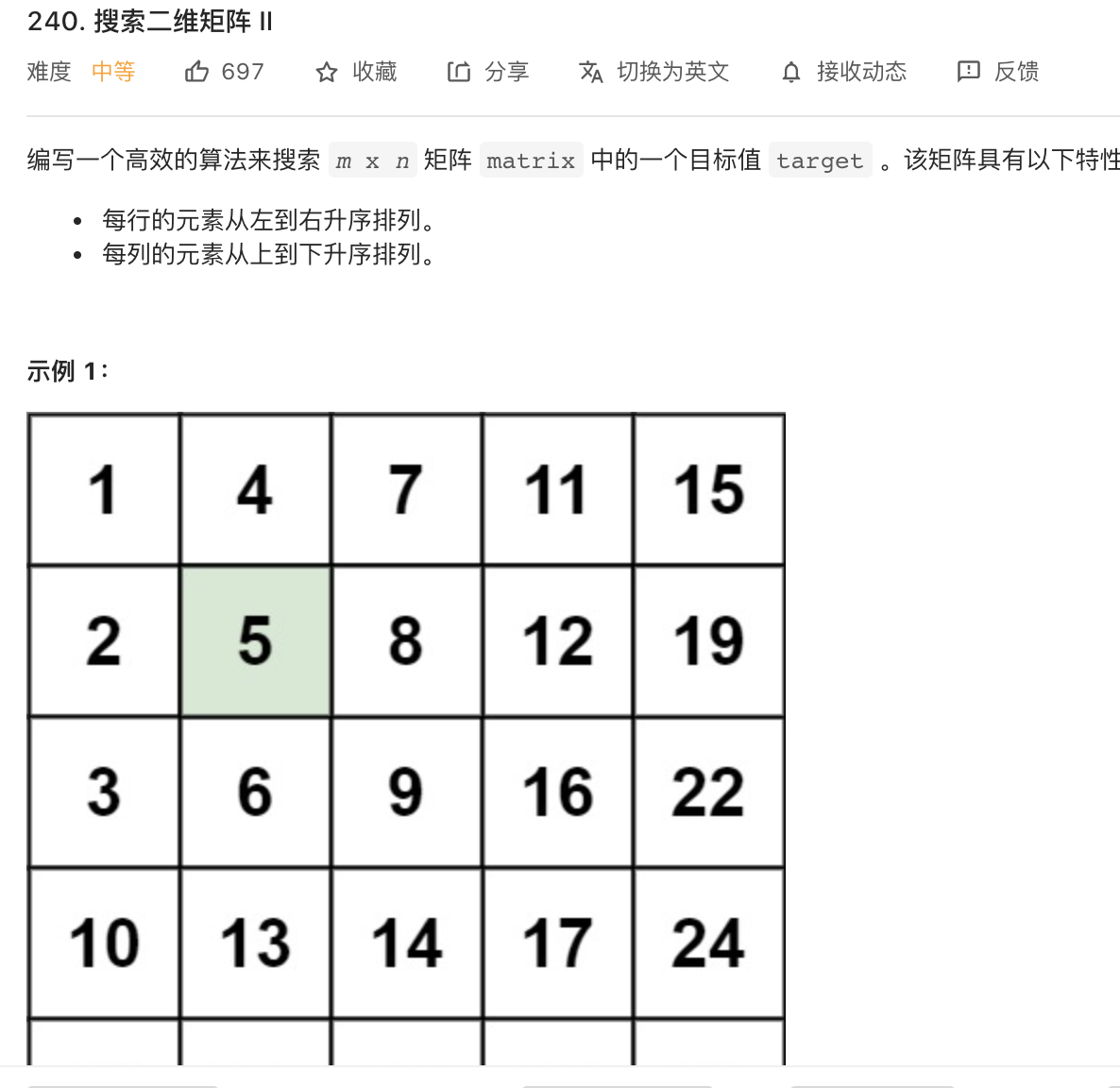
43. 搜索二维矩阵|| （技巧）

https://leetcode-cn.com/problems/search-a-2d-matrix-ii/

image-20210823163054226

发现到左下角的元素比上面所有元素大，比右边所有元素小，所以以左下角为标准来不断缩小矩阵。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length;
        int n = matrix[0].length;

        if (m <= 0 || n <= 0) {
            return false;
        }
        int i = m - 1;
        int j = 0;
        while (i >= 0 && j < n) {
            if (matrix[i][j] == target) {
                return true;
            }
            if (matrix[i][j] < target) {
                j++;
            }else {
                i--;
            }

        }
        return false;
    }
}

44.用rand7()实现rand10()

https://leetcode-cn.com/problems/implement-rand10-using-rand7/

image-20210823212951396

第一种方法：十分之一 = 二分之一 * 五分之一。

二分之一：当a为奇或者为偶，那么rand7怎么实现？当ran7 = 7的时候，重新rand即可保证落在1-6之间，那么奇偶都为1/2.

五分之一：当b大于5的时候，重新rand即可保证落在1-5之间。

概率相乘：奇数的时候返回1-5，偶数的时候返回6-10，这样保证每个数概率都是1/10.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * The rand7() API is already defined in the parent class SolBase.
 * public int rand7();
 * @return a random integer in the range 1 to 7
 */
class Solution extends SolBase {
    public int rand10() {
        // 1/10 = 1/2 * 1/5
        int a = rand7();
        int b = rand7();
        // 1-6奇偶平均
        while (a == 7) {
            a = rand7();
        }
        // 1-5: 1/5的概率平均
        while (b > 5) {
            b = rand7();
        }
        // 如果a是偶数，那么范围在1-5之间，如果a是奇数，范围在6-10之间。a出现奇偶的概率：1/2
        // b出现1-5: 1/5，
        return ((a & 1) == 0 ? 0 : 5) + b;
    }
}

45.括号生成（DFS）

https://leetcode-cn.com/problems/generate-parentheses/

image-20210824171053663 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    List<String> list = new ArrayList<>();
    public List<String> generateParenthesis(int n) {
        dfs(n,n, "");
        return list;
    }
        // left，right分别代表还需要添加几个左括号/右括号。
    public void dfs(int left, int right, String res ) {
        if (left == 0 && right == 0) {
            list.add(res);
            return;
        }
        if (left > 0) {
            dfs(left - 1, right, res + "(");
        }
      // 只有左边有左括号，才能加右括号
        if (right > left) {
            dfs(left, right - 1, res + ")" );
        }
    }
}

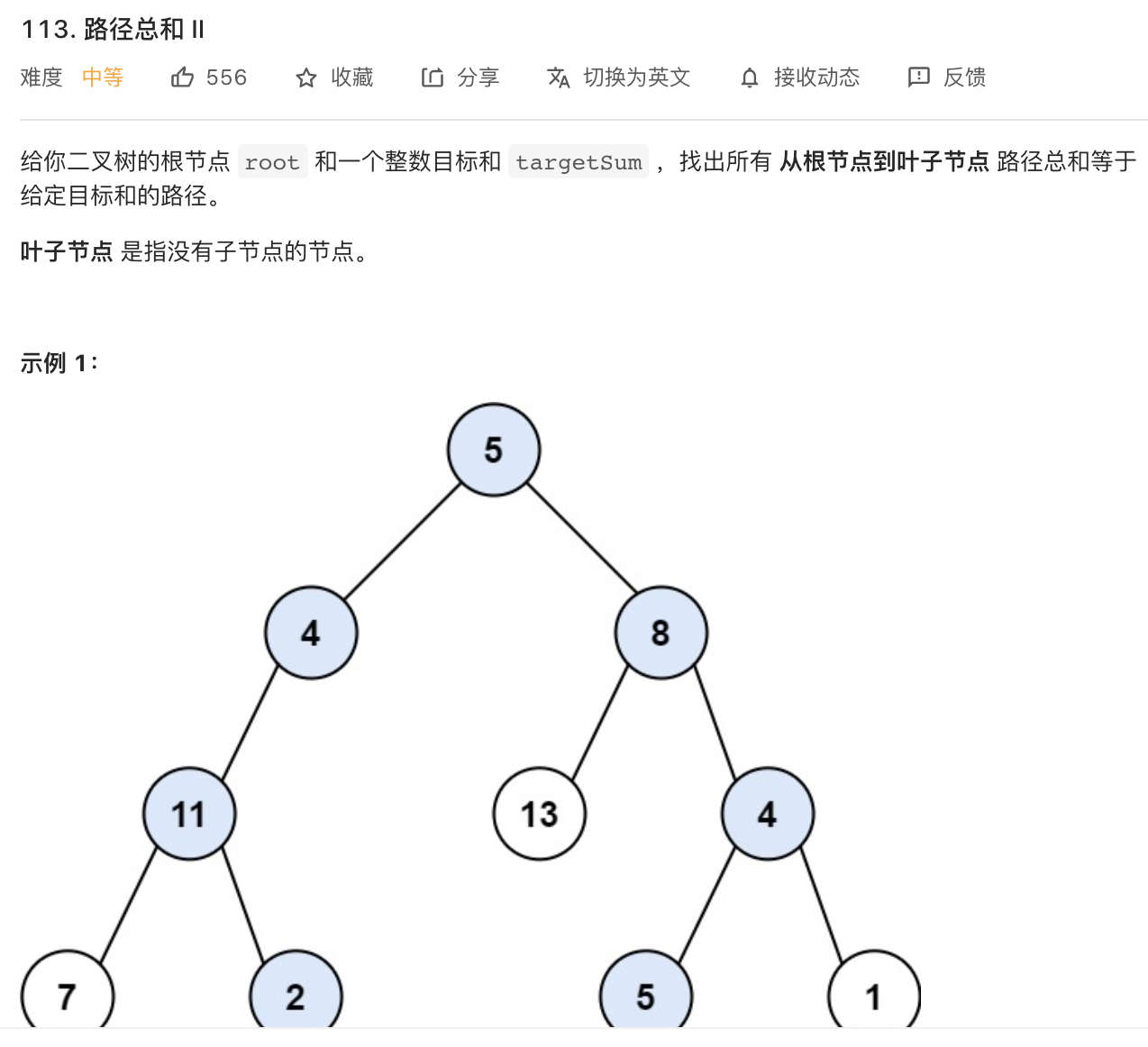
46.路径总和||（DFS）

image-20210824174958415 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    List<List<Integer>> res = new ArrayList<>();
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        dfs (root, targetSum, 0, new LinkedList<Integer>());
        return res;
    }

    public void dfs(TreeNode root, int targetSum, int curSum, LinkedList<Integer> track) {
        if (root == null ) return;
        // 当到达符合条件的叶子节点时，还没有把值加进去，所以需要内部加
        if (root.left == null && root.right == null && targetSum == curSum + root.val) {
            track.add(root.val);
            res.add(new LinkedList(track));
            track.removeLast();
            return;
        }
        track.add(root.val);
        dfs (root.left, targetSum, curSum + root.val, track);
        dfs (root.right, targetSum, curSum + root.val, track);
        track.removeLast();
    }
}

47.快排与归并排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
public void quickSort(int[] nums, int left, int right) {
    if (left >= right) return;
    int i = left;
    int j = right;
    int base = nums[left];
    while (i < j) {
        while (i < j && nums[j] >= base) {
            j--;
        }
        nums[i] = nums[j];
        while (i < j && nums[i] <= base) {
            i++;
        }
        nums[j] = nums[i];
    }
    nums[i] = base;
    quickSort(nums, left, i - 1);
    quickSort(nums,i + 1, right);
}

public void mergeSort(int[] nums, int left, int right) {
    int mid = (left + right) / 2;
    if (left < right) {
        // 二分进入左边
        mergeSort(nums,left, mid);
        // 二分进入右边
        mergeSort(nums, mid + 1, right);

        // 合并
        merge(nums, left, mid, right);
    }
}

public void merge(int[] nums, int left, int mid, int right) {
    int[] temp = new int[right - left + 1];

    int i = left;
    int j = mid + 1;
    int k = 0;
    // 把较小的数 移动到新数组.不要忘记 = 
    while (i <= mid && j <= right) {
        // 合并两个有序数组
        if (nums[i] < nums[j]) {
            temp[k++] = nums[i++];
        }else {
            temp[k++] = nums[j++];
        }
    }

    // 把左边剩余的数移入数组
    while (i <= mid) {
        temp[k++] = nums[i++];
    }
    // 把右边剩余的数移入数组
    while (j <= right) {
        temp[k++] = nums[j++];
    }
    // 覆盖到nums
    for(int m = 0; m < temp.length; m++) {
        nums[left + m] = temp[m];
    }
}

48.零钱兑换||(动态规划)

image-20210825174408582

完全背包的组合问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    // dp[i]:凑成金额为i有多少种方式
    // dp[i] += dp[i - coins[j]] 
    public int change(int amount, int[] coins) {
        int n =coins.length;
        if (n == 0) return 0;
        int[] dp = new int[amount + 1];
        dp[0] = 1;
                // 从coin开始遍历避免了出现1，2 2，1的重复
        for (int coin : coins) {
            for (int i = 0; i+coin <= amount; i++) {
                dp[i+coin] += dp[i];
            }
        }
        return dp[amount];
    }
}

49. 最大子序和（动态规划）

image-20210825223733118 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    // dp[i] : 0-i 的最大和
    // dp[i] = max(dp[i - 1] + nums[i], nums[i]);
    public int maxSubArray(int[] nums) {
        if (nums.length == 0) return 0;
        int[] dp = new int[nums.length];
        int res = nums[0];
        dp[0] = nums[0];
        for (int i = 1; i < nums.length; i++) {
            dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
            res = Math.max(dp[i], res);
        }

        return res;
    } 
}

50.组合总数（DFS）

https://leetcode-cn.com/problems/combination-sum/

image-20210825225633075

回溯法,首先先对数组进行排序，便于之后进行剪枝（大于target直接break）。

对于非重复，之前是对track进行排序然后看是否存在，存在就不添加，非常消耗性能，且慢。

可以使用begin来表示下一次递归从哪里开始，由于可以重复使用，所以begin = i。同理如果每个元素只能使用一次，那么begin就 = i+1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    List<List<Integer>> res = new ArrayList<>();
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        LinkedList<Integer> track = new LinkedList<>();
        Arrays.sort(candidates);
        backTrack(candidates,target, 0, track,0);
        return res;
    }

    public void backTrack(int[] candidates, int target,int curSum,LinkedList<Integer> track, int begin) {
        if (curSum > target) {
            return;
        }
        if (target == curSum) {
            res.add(new LinkedList(track));
            return;
        }

        for (int i = begin; i < candidates.length; i++) {
            if (candidates[i] > target) break;
            track.add(candidates[i]);
            // 从begin开始，由于可以选择多次，之前的都不会选择，自动去重
            backTrack(candidates, target, curSum + candidates[i], track, i);
            track.removeLast();
        }

    }
}

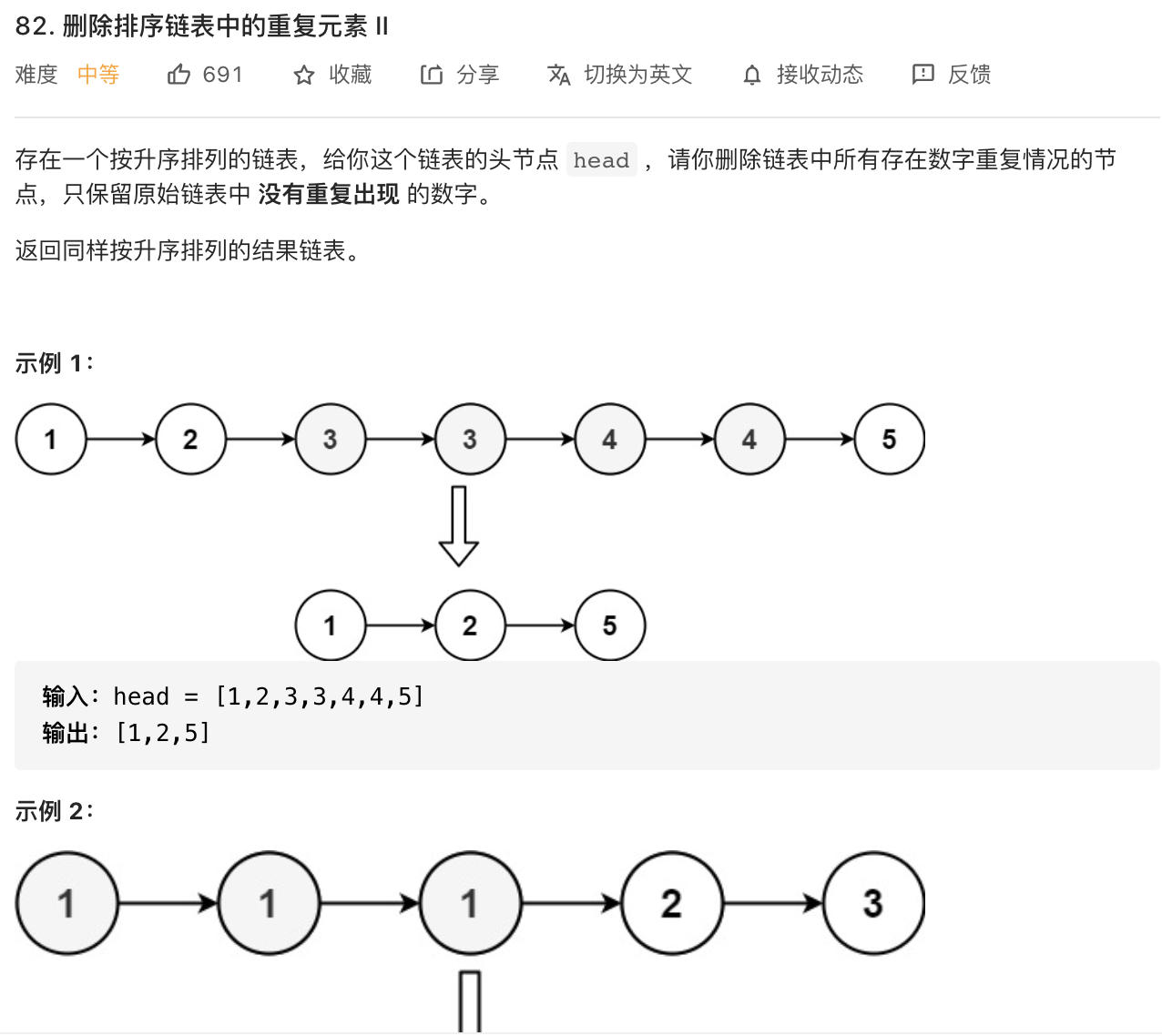
51.删除排序链表中重复的元素||（双指针）

https://leetcode-cn.com/problems/remove-duplicates-from-sorted-list-ii/

image-20210827155609093

思路即用三个变量pre、cur、next进行遍历。

当cur.val == next.val的时候，next = next.next;

然后把pre.next = next;

如果不重复，则都往后走

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public ListNode deleteDuplicates(ListNode head) {
        if (head == null) return null;
        ListNode dummy = new ListNode(0);
        dummy.next = head;

        ListNode pre = dummy;
        ListNode cur = head;
        ListNode next = cur.next;

        while (cur != null && next != null) {
            // 不重复，往后走
            if (next != null && cur.val != next.val) {
                pre = cur;
                cur = next;
                next = cur.next;
                continue;
            }
            // 重复了
            while (next != null && cur.val == next.val){
                next = next.next;
            }
            pre.next = next;
            cur = next;
          // 这里next可能为null，所以多判断了一次
            if (cur == null) break;
            next = cur.next;
        }
        return dummy.next;
    }
}

52.字符串相加（大数加法）

https://leetcode-cn.com/problems/add-strings/

image-20210827163023769

大数加法，不能将字符串转成数字然后相加，会导致溢出。

所以根据小学学的竖式加法，从后往前一位一位地相加，所以重点考虑进位。

如果两个数相加 >10,进位

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public String addStrings(String num1, String num2) {
        StringBuilder res = new StringBuilder("");
        int i = num1.length() - 1, j = num2.length() - 1, carry = 0;
        while(i >= 0 || j >= 0){
            int n1 = i >= 0 ? num1.charAt(i) - '0' : 0;
            int n2 = j >= 0 ? num2.charAt(j) - '0' : 0;
            // 两位数之和，注意加了carry，不用关心上一次的进位
            int tmp = n1 + n2 + carry;
              // 是否产生进位，如果产生进位会加到下一次中
            carry = tmp / 10;
              // 总是加上%10的数
            res.append(tmp % 10);
            i--; j--;
        }
        // 最前面一位相加进位，如64 + 47 = 101
        if(carry == 1) res.append(1);
      // 最后反转
        return res.reverse().toString();
    }
}

53.二叉树的完全性校验

https://leetcode-cn.com/problems/check-completeness-of-a-binary-tree/

image-20210827172954082

使用BFS，一层一层地加入到队列中，如果遇到null节点，继续遍历后面节点看是否有非空节点，如果有的话就不是完全二叉树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public boolean isCompleteTree(TreeNode root) {
        if (root == null) {
            return false;
        }

        Queue<TreeNode> q = new LinkedList<>();
        q.offer(root);
        while (!q.isEmpty()) {
            int size = q.size();
            TreeNode res = q.poll();
            // 如果节点不为null，添加每个节点的左右子树
            if (res != null) {
                q.offer(res.left);
                q.offer(res.right);
            }else {
                // 否则遍历剩下节点查看是否有非空节点
                while (!q.isEmpty()) {
                    res = q.poll();
                    if (res != null) {
                        return false;
                    }
                }
            }
        }
        return true;
    }
}

54.买卖股票的最佳时机||(贪心、DP)

https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-ii/

image-20210827175233102

题目意思即给定数组，卖出后又可以买入，找到可以获得的利润最大值。

常规思维即对于【1，2，3，4，5】，在第一天买入，最后一天卖出。

但是需要判断在什么时候卖出，就会变得复杂。

使用贪心思想，只要今天比昨天大就卖出，然后今天又买入。

依次循环，使用贪心思想就得到了最大的利润。

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {

    public int maxProfit(int[] prices) {
        int res = 0;
        for (int i = 1; i < prices.length; i++) {
            if (prices[i] > prices[i - 1]) {
                res += prices[i] - prices[i - 1];
            }
        }
        return res;
    }
}

55.最长连续序列

https://leetcode-cn.com/problems/longest-consecutive-sequence/

image-20210829214115973

题目要求O(n)复杂度，所以不能进行排序，通常我们用空间去换时间，或者时间去换空间。

这道题我们用哈希表来解决。

解决思路即：1、将每个元素加入到哈希Set中。

2、遍历每个元素，遍历一个删除一个。

3、如果删除成功，那么继续删除比大依次大1的元素，记录删除的个数，然后删除比他依次小1的个数，记录删除个数。如第一个示例，遍历到4的时候，删除4，然后依次删除掉3，2，1，由于没有5，所以与4相临的都删除完了，再记录删除的长度即相临的个数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
    public int longestConsecutive(int[] nums) {
        if (nums.length <= 0) {
            return 0;
        }
        Set<Integer> set = new HashSet<>();

        for (int num : nums) {
            set.add(num);
        }
        int longest = 0;

        for (int num : nums) {
            // 如果能删除成功，说明存在
            if (set.remove(num)) {
                // 向左查找
                int left = 0;
                int right = 0;
              // 用来删除左右两边的数
                int leftNum = num;
                int rightNum = num;
              // 删除比num小的数
                while (set.remove(leftNum - 1)) {
                    left++;
                    leftNum--;
                }
              // 删除比num大大数
                while (set.remove(rightNum + 1)) {
                    right++;
                    rightNum++;
                }
                longest = Math.max(longest, right + left + 1);
            }
        }
        return longest;
    }
}

56.航班预订统计（差分数组）

https://leetcode-cn.com/problems/corporate-flight-bookings/

image-20210831231401000

差分数组：第i项是第i-1项-第i项得到，反之依次累加就可以得到原数组。

对第一个示例：

[10,0 , -10, 0, 0]

[10, 20, -10, -20, 0]

[10, 45, -10, -20, 0]

即差分数组。

前缀和累加起来

[10, 55, 45, 25, 25],得到最终结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int[] corpFlightBookings(int[][] bookings, int n) {
        int[] nums = new int[n];
        for (int[] booking : bookings) {
            nums[booking[0] - 1] += booking[2];
            if (booking[1] < n) {
                nums[booking[1]] -= booking[2];
            }
        }
        for (int i = 1; i < n; i++) {
            nums[i] += nums[i - 1];
        }
        return nums;
    }
}

57.前序中序建立二叉树（递归，字节二面）

https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/

image-20210909105705751

字节二面的算法题，之前试着做过这个题，但是当时有些烦躁就没做完，心里赌他不会考，结果考到了，赌狗biss。

正常思维还是很容易：前序序列第一个是root，然后去中序序列找root的索引，左边的都是左子树，右边的都是右子树。

然后依次递归，先构建左子树，前序序列第二个是根节点，然后去中序序列左边区域找root索引。

对于任意一颗树而言，前序遍历的形式总是

[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ] 即根节点总是前序遍历中的第一个节点。而中序遍历的形式总是

[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    Map<Integer, Integer> map = new HashMap<>();
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        for (int i = 0 ; i < inorder.length; i++) {
            map.put(inorder[i], i);
        }
        int n = preorder.length;
        return build(preorder, inorder, 0, n - 1, 0 , n - 1);
    }

      // 前两个参数是两个序列，后面四个参数是前序的左右边界和中序的左右边界
    public TreeNode build(int[] preorder, int[] inorder, int preLeft, int preRight, int inLeft, int inRight) {
        if (preLeft > preRight) {
            return null;
        }
        // 根节点索引
        int preOrderRootIdx = preLeft;
        // 中序中定位
        int inOrderRootIdx = map.get(preorder[preOrderRootIdx]);

        // 根节点
        TreeNode root = new TreeNode(preorder[preOrderRootIdx]);

        // 左子树节点数目
        int leftSize = inOrderRootIdx - inLeft;
        // 递归构造左子树
          // preLeft + 1除去根节点，preLeft + leftSize 表示前序序列中所有左子树的右边界，inLeft 表示中序中左子树的开始索引，inOrderRootIdx - 1表示到根节点前所有左子树索引
        root.left = build(preorder, inorder, preLeft + 1, preLeft + leftSize, inLeft, inOrderRootIdx - 1);
        // 递归构造右子树
        root.right = build(preorder, inorder, preLeft + leftSize + 1, preRight, inOrderRootIdx + 1, inRight);
        return root;
    }
}

58.二叉树的最大宽度（BFS）

https://leetcode-cn.com/problems/maximum-width-of-binary-tree/

image-20210909150732610

首先想到的是层序遍历，如果为null也存入进去，最后从后往前和从前往后第一个遍历到的非null节点的索引相减即该层的宽度。

但是实施的时候出现了问题：1、null节点也添加，每层null的左右孩子节点也添加null，怎么判断是否结束？只有遍历每层都是null的时候说明树到底了，时间复杂度高，且如果树缺的很多，那么会添加很多null节点。

2、计算宽度的时候需要从后往前和从前往后，节点数只有一个的时候这个边界需要额外判断，且空间复杂度比较高，时间复杂度也比较高。

联想二叉树排列的性质，如果根节点在该层第i个，那么他左孩子节点在下一层的第2*i个，

右孩子节点在下一层的第2*i + 1个。这样遍历每个节点的时候给左右孩子节点标记一个pos，该层遍历完后用最后一个节点的pos-第一个节点的pos即可得到最大宽度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int widthOfBinaryTree(TreeNode root) {
        if (root == null) return 0;
        return bfs(root);
    }

    public int bfs(TreeNode root) {
        int max = 1;
        Queue<TempNode> q = new LinkedList<>();
        q.offer(new TempNode(root,0, 0));
        int curDepth = 0, left = 0, res = 0;
        while (!q.isEmpty()) {
            TempNode a = q.poll();
            if (a.node != null) {
                // 每层左边第一个节点pos都为0，左孩子节点次序为第2*pos。
                q.offer(new TempNode(a.node.left,a.depth + 1, a.pos * 2));
                // 节点的右节点在下一层的位置是2 * pos + 1；
                q.offer(new TempNode(a.node.right,a.depth + 1, a.pos * 2 + 1));
                // curDepth指示当前层数，不相等时说明上一层已遍历完，层数+1，left为下一层第一个节点的pos
                if (curDepth != a.depth) {
                    curDepth = a.depth;
                    left = a.pos;
                }
                res = Math.max(res, a.pos - left + 1);
            }
        }
        return res;
    }


    class TempNode {
        TreeNode node;
      // 该节点的深度
        int depth;
      // 该节点在该层的位置
        int pos;
        public TempNode(TreeNode node, int depth, int pos) {
            this.node = node;
            this.depth = depth;
            this.pos = pos;
        }
    }
}

59.二叉树展开为链表（递归）

https://leetcode-cn.com/problems/flatten-binary-tree-to-linked-list/

image-20210909152627066 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public void flatten(TreeNode root) {
        dfs(root);
    }
    TreeNode pre = null;
    public void dfs(TreeNode root) {
        if (root == null) {
            return;
        }
      // 先dfs到右子树，再dfs左子树，pre记录上一个节点
        dfs(root.right);
        dfs(root.left);
      // 链接到右子树上
        root.right = pre;
      // 记得将左子树置空
        root.left = null;
        pre = root;
    }
}

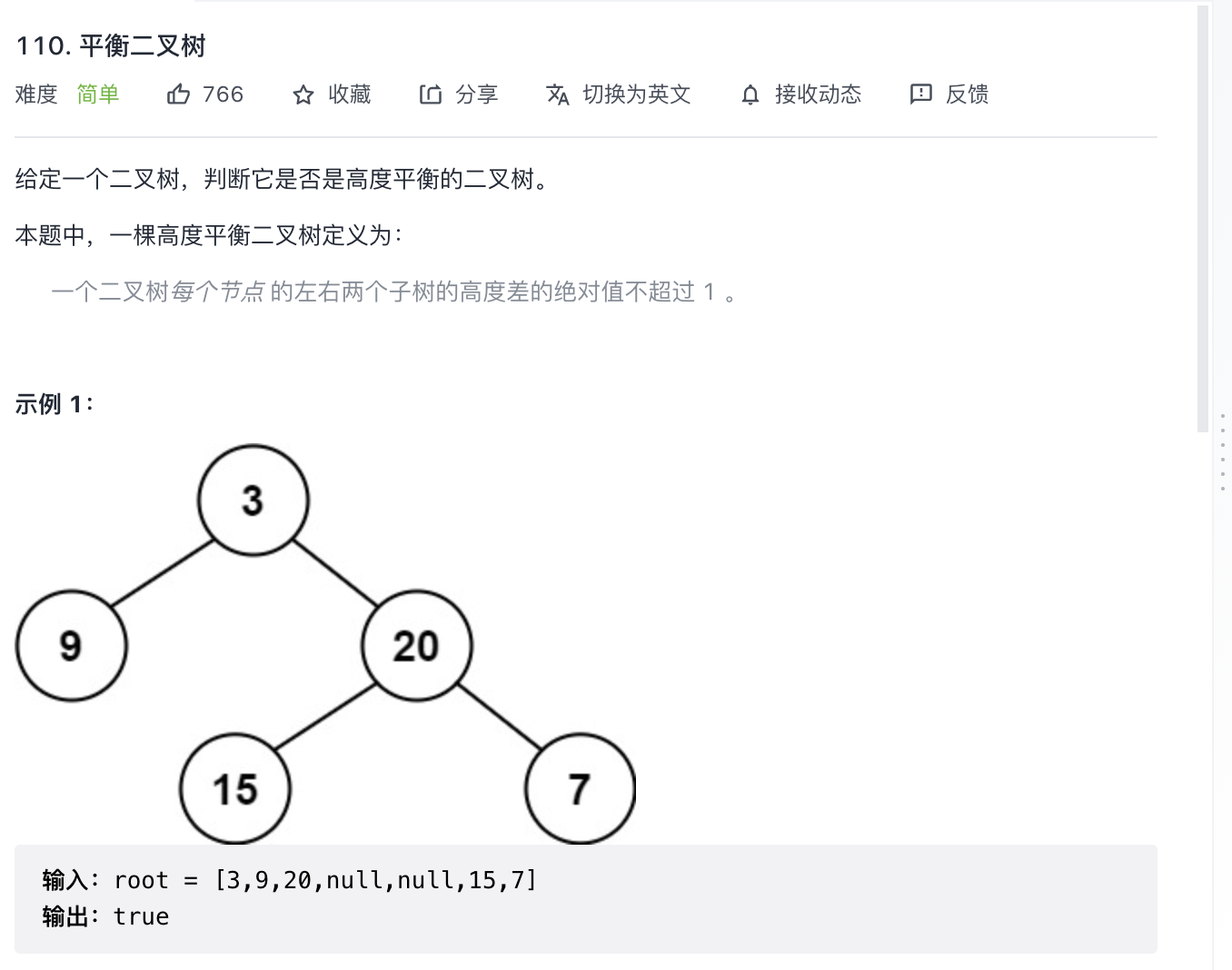
59.平衡二叉树（递归）

image-20210909174543593

对于root，递归函数返回子树最大高度，如果最大高度之差超过1就将res置为false，最后直接返回res

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    boolean res = true;
    public boolean isBalanced(TreeNode root) {
        dfs(root, 0);
        return res;
    }

    public int dfs (TreeNode root, int level) {
      // 剪枝后100%
        if (!res) {
            return 0;
        }
        if (root == null) {
            return level;
        }
        int left = dfs(root.left, level + 1);
        int right = dfs(root.right, level + 1);
        if (Math.abs(right - left) > 1) {
            res = false;
        }
        return Math.max(left, right);
    }
}

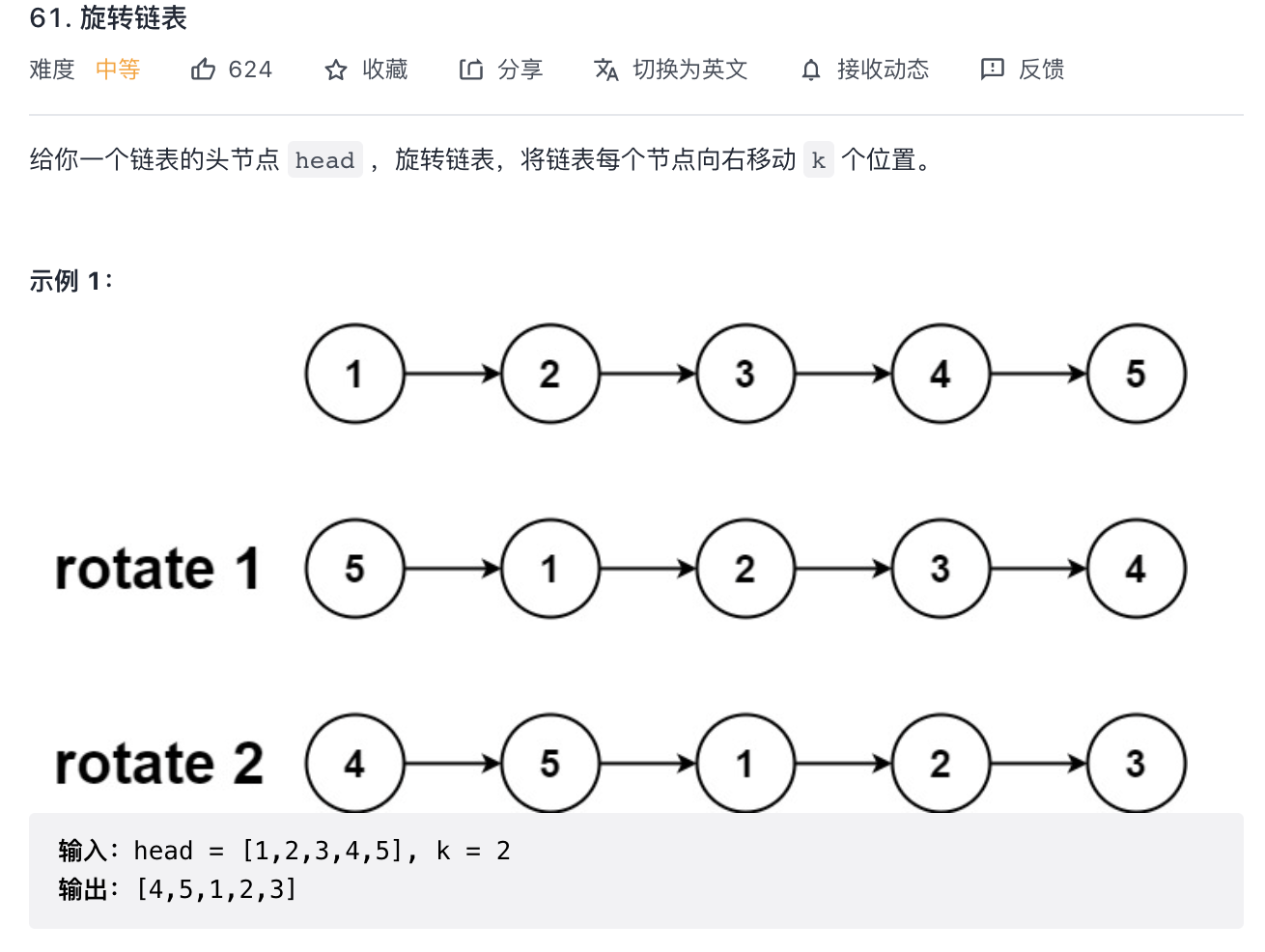
60.旋转链表（链表）

image-20210910151236993

向右移动k个位置，即将后k个节点接到head前面

如1 2 3 4 5， k=2

即将后两个节点4 5 接到1前面即可。

对于k > 链表长度，进行取模。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
    public ListNode rotateRight(ListNode head, int k) {
        if (head == null || head.next == null) return head;
        int count = getCount(head);
      // k取模减少无效循环
        k = k >= count ? k % count : k;
        if (k == 0) return head;
        return getApartNode(head,k);
    }   


    public ListNode getApartNode(ListNode head, int k) {
        ListNode pre = head;
        ListNode left = head;
        ListNode right = head;
        for (int i = 0; i < k - 1 && right.next != null; i++) {
            right = right.next;
        }
        while (right.next != null) {
            pre = left;
            left = left.next;
            right = right.next;
        }
        // pre:断开新尾结点后面的链表
        // left:新头结点
        // right:head 的前一个节点
        pre.next = null;
        right.next = head;
        return left;

    }
    public int getCount(ListNode head) {
        int count  = 1;
        ListNode cur = head;
        while (cur.next != null) {
            cur = cur.next;
            count++;
        }
        return count;
    }
}