二叉排序树的创建、搜索与遍历
二叉排序树(Binary Sort
Tree)又叫二叉查找树。平衡二叉树（AVL树）、B树、B+树、红黑树都能看到二叉排序树的思想，所以说二叉排序树是学习后面树的基础也不为过。
二叉排序树主要具有以下的三个特征：
- 若左子树不空，则左子树上所有结点的值均小于或等于它的根结点的值；
- 若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值；
- 左、右子树也分别为二叉排序树；
这个定义读下来直观的感受就是递归。整棵树具有前两个特点，任何子树也具有前两个特点。
直接上代码：
数据结构
树的结点定义为TreeNode类。
| public class TreeNode {
public Integer data;
public TreeNode parent;
public TreeNode left;
public TreeNode right;
public TreeNode(Integer data){
this.data = data;
}
@Override
public String toString() {
return "TreeNode [data=" + data + "]";
}
}
|
整棵树定义为BSTree类
| public class BSTree {
public TreeNode root;
public Integer size = 0;
public TreeNode getRoot() {
return root;
}
public Integer getSize() {
return size;
}
}
|
创建二叉排序树
采用的策略：
- 判断根节点是否为null，为null则创建根节点。
- 如果存在父节点，则判断该结点和父节点比较值大小
- 如果比父节点小，判断父节点左子树是否为空，为空则插入到左子树
- 如果比父节点大，判断父节点右子树是否为空，为空则插入到右子树
- 相等值不插入
代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| public Boolean add(Integer data) {
if (null == root) {
root = new TreeNode(data);
System.out.println("根结点创建成功，值为：" + data);
return true;
}
TreeNode node = new TreeNode(data);
TreeNode currentNode = root;
TreeNode parentNode;
while (true) {
parentNode = currentNode;
if (node.data < parentNode.data) {
currentNode = currentNode.left;
if (null == currentNode) {
parentNode.left = node;
node.parent = parentNode;
System.out.println(data + " 成功插入到 " + parentNode.data + " 的左子树");
size++;
return true;
}
} else if (node.data > parentNode.data) {
currentNode = currentNode.right;
if (null == currentNode) {
parentNode.right = node;
node.parent = parentNode;
System.out.println(data + " 成功插入到 " + parentNode.data + " 的右子树");
size++;
return true;
}
} else {
System.out.println(data + "已存在！不能重复插入");
return false;
}
}
}
|
查找结点
采用策略：
- 如果根节点为null，直接返回。
- 如果根节点不为空，判断当前结点(currentNode)是否为null，不为null则比较大小
- 如果要查找的值比当前结点值小，则去左子树查找
- 如果要查找的值比当前结点值大，则去右子树查找
- 找到则返回，找不到返回null
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| public TreeNode searchBST(Integer data) {
if (null == root) {
return null;
}
TreeNode currentNode = root;
while (currentNode != null) {
if (data < currentNode.data) {
currentNode = currentNode.left;
} else if (data > currentNode.data) {
currentNode = currentNode.right;
} else {
return currentNode;
}
}
return null;
}
|
前序遍历
前序遍历相对来说比较简单。
递归前序遍历
| public void preOrderRecursivePrint(TreeNode node) {
if (null != node) {
System.out.print(node.data + " ");
}
if (node.left != null) {
preOrderRecursivePrint(node.left);
}
if (node.right != null) {
preOrderRecursivePrint(node.right);
}
}
|
迭代前序遍历
迭代替代递归的思想在于用自定义栈替代了系统的方法栈，其实思想都差不多。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public void preOrderIterationPrint(TreeNode node) {
if (null != node) {
Stack<TreeNode> stack = new Stack<>();
stack.push(node);
while (!stack.isEmpty()) {
TreeNode pop = stack.pop();
System.out.print(pop.data + " ");
if (pop.right != null) {
stack.push(pop.right);
}
if (pop.left != null) {
stack.push(pop.left);
}
}
}
}
|
中序遍历
递归中序遍历
| public void midOrderRecursivePrint(TreeNode node) {
if (null != node) {
if (node.left != null) {
midOrderRecursivePrint(node.left);
}
System.out.print(node.data + " ");
if (node.right != null) {
midOrderRecursivePrint(node.right);
}
}
}
|
迭代中序遍历
迭代的中序遍历相比之下复杂一些，在左孩子结点、根节点、右孩子节点顺序之下，根节点也可看作其父结点的左孩子结点或右孩子结点。所以不需要针对根节点进行特殊操作。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| public void midOrderIterationPrint(TreeNode node) {
if (null != node) {
Stack<TreeNode> stack = new Stack<>();
TreeNode currentNode = node;
while (currentNode != null || !stack.isEmpty()) {
while (currentNode != null) {
stack.push(currentNode);
currentNode = currentNode.left;
}
if (!stack.isEmpty()) {
currentNode = stack.pop();
System.out.print(currentNode.data + " ");
currentNode = currentNode.right;
}
}
}
}
|
后序遍历
递归后序遍历
| public void postOrderRecursivePrint(TreeNode node) {
if (node != null) {
if (node.left != null) {
postOrderRecursivePrint(node.left);
}
if (node.right != null) {
postOrderRecursivePrint(node.right);
}
System.out.print(node.data + " ");
}
}
|
迭代后序遍历
迭代后序遍历比较复杂。由于先将左子树全部入栈，再一个个退栈后，不会立即输出退栈的结点值，还需要查找其是否有右孩子结点，所以需要重新压入栈。所以如果当其再次退栈后又会回到原来的右子树形成死循环，所以需要一个临时结点记录右孩子结点（rightNode）的值防止出现重复遍历。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| public void postOrderIterationPrint(TreeNode node) {
if (node != null) {
Stack<TreeNode> stack = new Stack<>();
TreeNode currentNode = node;
TreeNode rightNode = null;
while (currentNode != null || !stack.isEmpty()) {
while (currentNode != null) {
stack.push(currentNode);
currentNode = currentNode.left;
}
currentNode = stack.pop();
while (currentNode != null && (currentNode.right == null || currentNode.right == rightNode)) {
System.out.print(currentNode.data + " ");
rightNode = currentNode;
if (stack.isEmpty()) {
System.out.println();
return;
}
currentNode = stack.pop();
}
stack.push(currentNode);
currentNode = currentNode.right;
}
}
}
|
运行结果
测试代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| public static void main(String[] args) {
BSTree tree = new BSTree();
int[] ints = ArrGenerator.generateArr(10, 100);
System.out.print("====要插入的值为：");
ArrGenerator.printArr(ints);
Arrays.stream(ints).forEach(tree::add);
System.out.print("====查找的值为：" + ints[3]);
System.out.println(tree.searchBST(ints[3]).toString());
System.out.print("====递归前序遍历：");
tree.preOrderRecursivePrint(tree.getRoot());
System.out.println();
System.out.print("====非递归前序遍历：");
tree.preOrderIterationPrint(tree.getRoot());
System.out.println();
System.out.print("====递归中序遍历：");
tree.midOrderRecursivePrint(tree.getRoot());
System.out.println();
System.out.print("====非递归中序遍历：");
tree.midOrderIterationPrint(tree.getRoot());
System.out.println();
System.out.print("====递归后序遍历：");
tree.postOrderRecursivePrint(tree.getRoot());
System.out.println();
System.out.print("====非递归后序遍历：");
tree.postOrderIterationPrint(tree.getRoot());
}
|
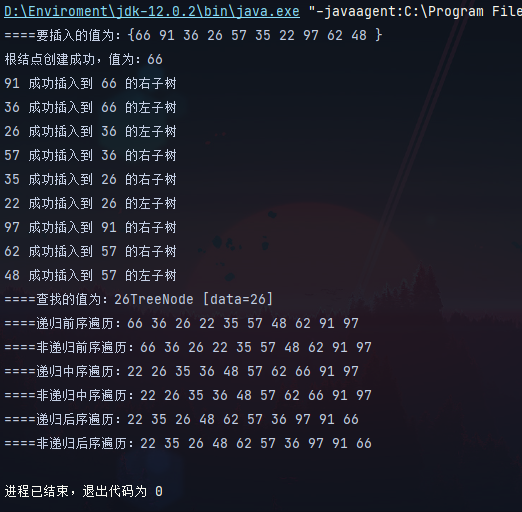image-20210402215203977
根据结果我们可以检查是否正确，预期整棵树应该为：
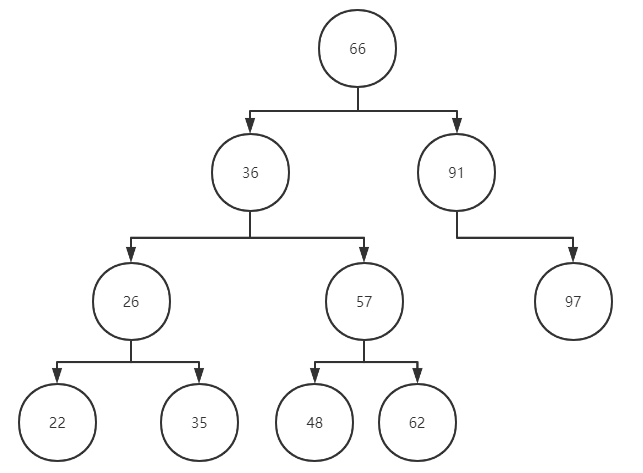image-20210402215550750
查看打印出来的插入结果完全符合。
小结
二叉排序树其实并不是很难，因为还没有涉及到平衡（旋转左右子树），而红黑树可以在10亿的数据里查找30次即可找到！背后的基础是基于平衡二叉树、而平衡二叉树是基于二叉排序树。所以想要手撕红黑树（梦想），只得基础先打牢。